VI. Charakteristik der Kollektivgegenstände durch ihre
Bestimmungsstücke oder sog. Elemente.


    § 38. Gehen wir auf die schon früher (Kap. II) bezüglich der Charakteristik der K.-G. gemachten allgemeinen Bemerkungen jetzt etwas bestimmter ein.

    Sollte ein K.-G. vollständig nach Maß und Zahl bestimmt sein, so würde es überhaupt gelten, nicht nur alle gegenwärtigen, sondern auch gewesenen und künftigen Exemplare desselben zu zählen und von jedem das Maß nach den Hinsichten zu nehmen, die einer quantitativen Bestimmung Raum geben, als wie Größe nach den drei Hauptdimensionen, Gewicht, Dichtigkeit, Dauer. Dies ist im allgemeinen unmöglich. Die Menge der Exemplare eines gegebenen Gegenstandes ist überhaupt meist unbestimmbar groß, und von dieser unbestimmbar großen Menge steht meist nur eine sehr beschränkte Anzahl für Maßnahmen daran zu Gebote. Dazu erhellt, daß, wenn z. B. das Gehirngewicht des Europäers und Negers verglichen werden soll, dies nicht dadurch geschehen kann, daß man die Gewichte von tausend europäischen Gehirnen den Gewichten von tausend Negergehirnen gegenüberstellt. Es gilt ein einheitliches Resultat. Also wird es zwar nach schon früher gemachten Bemerkungen gelten, so viele Exemplare der zu untersuchenden und zu vergleichenden Gegenstände als möglich ohne willkürlichen Ausschluß gewisser Größen zu messen, worin man nicht zu viel tun kann, um unausgeglichenen Zufälligkeiten nicht zu viel Raum zu geben, die erhaltenen Maße in angegebener Weise nach Zahl und Größe in Verteilungstafeln zu ordnen, und, da dies aber doch erst dazu führt, den Gang der Werte im allgemeinen übersehen zu lassen, aus diesen Verteilungstafeln gewisse Werte, die sog. Bestimmungsstücke oder Elemente des K.-G. abzuleiten, welche eine Charakteristik des Gegenstandes und Möglichkeit seines Vergleiches mit anderen Gegenständen nach quantitativer Beziehung gewähren. In der Tat hat man hierin die Frucht der vielen einzelnen Maßbestimmungen zu sehen und zu bieten.

    Begnügt man sich nun, wie es häufig der Fall ist, mit der Angabe des arithmetischen Mittels eines K.-G., so hat man darin allerdings einen wichtigen und in keinem Falle zu vernachlässigenden Bestimmungswert und Vergleichswert mit anderen Gegenständen; aber es können zwei K.-G. ganz oder nahe darin übereinstimmen und doch nach anderen Beziehungen sehr auseinander weichen. Nun konnte es früher genug erscheinen, auch die mittlere Schwankungsgröße und ganze Schwankungsweite eines K.-G. durch Angabe der mittleren Abweichung vom arithmetischen Mittel und der Extreme zu berücksichtigen, um die wesentliche Charakteristik damit erschöpft zu haben, und in der Tat ist dies mitunter geschehen. Aber mit der Erkenntnis der den K.-G. in so großer Allgemeinheit und in so verschiedenem Grade nach einer oder der anderen Richtung zukommenden Eigenschaft der Asymmetrie ist das bisher nicht gefühlte Bedürfnis eingetreten, die K.-G., die man überhaupt einer eingehenden Untersuchung und Vergleichung wert hält, auch nach dieser Richtung zu charakterisieren, d. i. die verschiedenen Hauptwerte, deren Unterscheidbarkeit durch die Asymmetrie bedingt ist, und die Abweichungswerte bezüglich derselben ins Auge zu fassen, womit nicht gesagt ist, daß jeder Gegenstand an sich Interesse genug hat, um sich auf eine solche Erweiterung seiner Charakteristik einzulassen, indes jedenfalls in einer allgemeinen Kollektivmaßlehre darauf eingegangen werden muß.

    § 39. Wenn nun schon die allgemeine Kollektivmaßlehre nicht bei der früher gewohnten, beschränkten Berücksichtigung von A und der dazu in Beziehung stehenden Abweichungen stehen bleiben kann, und doch, wie schon oben zugegeben, nicht jeder K.-G. auf eine Berücksichtigung aller möglichen Bestimmungsstücke, die im II. Kapitel angegeben sind, Anspruch machen kann, so wird überhaupt nicht leicht Anlaß sein, auf eine allseitige Berücksichtigung derselben einzugehen, es sei denn bei einem K.-G., dem man eine ganz besondere Wichtigkeit beilegt, und der als Beispiel für die Durchführbarkeit der allseitigen Berücksichtigung selbst dienen soll. Also kann man leitende Gesichtspunkte für eine zu treffende Auswahl wünschen.

    Alles zusammengenommen nun glaube ich, daß, wo man mit Bestimmungen sparen will, und es eine Konvention gilt, an welchen Hauptwert man sich vorzugsweise zur charakteristischen Unterscheidung gegebener K.-G. halten soll, dem arithmetischen Mittel mit seinen Abweichungen immer der ihm bisher gewahrte Vorzug bleiben wird, nur daß man mit Übergehung der übrigen Bestimmungsstücke zugleich an Einsicht in die quantitative Konstitution der K.- G. verliert und Charaktere derselben außer Acht läßt, die an sich nicht minder bedeutsam sind, als die sich an das arithmetische Mittel knüpfen, und auf die Aufstellung eines allgemeinen Verteilungsgesetzes emporheben. Zur Klarstellung hiervon wird auf die schon oben (Kap. II) angegebenen Eigenschaften der verschiedenen Hauptwerte mit erweiternder und erläuternder Betrachtung zurückzukommen sein.

    [Dies wird ausführlich im X. Kap. geschehen. Während aber dort die Eigenschaften jedes einzelnen Hauptwertes für sich vorgeführt werden, handelt es sich hier um eine vergleichende Beurteilung der Hauptwerte selbst rücksichtlich ihrer Leistungen zur Charakteristik der K.-G. Aus diesem Grunde kommen bloß der arithmetische Mittelwert A, der Zentralwert C und der dichteste Wert D in Betracht; denn der Scheidewert R, sowie der schwerste Wert T und der Abweichungsschwerwert F sind von vornherein wegen ihrer geringeren Bedeutung bei einer zu treffenden Auswahl bei Seite zu lassen. Dabei ist jedoch ein Unterschied dazwischen zu machen, ob jene drei Hauptwerte mit Rücksicht auf ein als gültig vorausgesetztes Verteilungsgesetz oder ohne Rücksicht auf ein solches betrachtet werden sollen, da je nachdem eine ganz verschiedene Wertschätzung derselben Platz greift.]

    § 40. [Läßt man nämlich die Voraussetzung fallen, daß ein Verteilungsgesetz den Gang der z-Werte einer Verteilungstafel regelt, so ist die letztere prinzipiell nur als eine regellose Ansammlung von Werten aufzufassen, und es kann darum den Hauptwerten nur die Bedeutung zukommen, als Mittelwerte jenen regellosen Komplex in mehr oder minder zutreffender Weise zusammenzufassen und zu vertreten. Dann ist aber keinem Zweifel unterworfen, daß die Bestimmung des A wertvoller ist als diejenige des C oder des D. Denn A stellt als arithmetisches Mittel den Durchschnittswert dar, der tatsächlich an Stelle jedes einzelnen Wertes gesetzt werden kann, wenn dieselben zu einer Summe zusammengefaßt werden sollen. C dagegen gibt bloß die Wertmitte an, die eben so oft überschritten als unterschritten wird, und repräsentiert somit die Tafelwerte mit geringerer Zuverlässigkeit, weil es nicht wie A von der Summe, sondern nur von der Anzahl der beiderseitigen Abweichungen abhängt. D schließlich kann gar nicht als stellvertretender Mittelwert zugelassen werden, da es nur den empirisch dichtesten Wert in seiner durch kein Gesetz geregelten Zufälligkeit bezeichnet und seiner Lage nach nicht rechnerisch bestimmt, sondern bloß durch den Anblick der Tafel gefunden werden kann. Überhaupt ist sein tatsächliches Vorhandensein in einer regellos verlaufenden Tafel nur als ein glücklicher Zufall anzusehen, dem keine Wichtigkeit beizumessen ist.]

    [Anders ist es, wenn das Bestehen eines Verteilungsgesetzes angenommen wird. Dann behält zwar A die Bedeutung als Durchschnittswert, die es auch in der regellosen Tafel hat, ohne direkt etwas zu gewinnen. Die Bedeutung von C dagegen wird größer, da es, mit Rücksicht auf die nunmehr in Kraft tretenden Wahrscheinlichkeitsbegriffe, als Wertmitte den wahrscheinlichen Wert darstellt. In den Mittelpunkt des Interesses rückt aber D, da es als empirisch dichtester Wert, wenigstens angenähert, d. h. von den unausgeglichenen Zufälligkeiten abgesehen, denjenigen Wert bezeichnet, dem die größte W. zukommt. D steht somit in solidarischem Zusammenhange mit dem Verteilungsgesetze, dessen Maximalwert prinzipiell mit ihm zusammenfallen muß. Auch erhellt unmittelbar, daß nach Aufstellung eines zutreffenden Verteilungsgesetzes ein doppelter Weg zur Bestimmung von D offen steht: der eine auf Grund des Gesetzes, dessen Maximalwert theoretisch den wahrscheinlichsten Wert bezeichnet; der andere auf Grund der Tafel, deren dichtester Wert empirisch den wahrscheinlichsten Wert angibt. Dabei ist es gleichgültig, ob der Gang der z in der Tafel den dichtesten Wert direkt oder nur die Tendenz zur Erzeugung eines solchen erkennen läßt. Denn infolge des in Kraft getretenen Gesetzes stehen die a und die z in funktionalem Zusammenhange, so daß nach bekannten Regeln das dichteste z durch Interpolation aus den gegebenen Tafelwerten berechnet werden kann, wenn seine rohe Bestimmung aus dem unmittelbaren Anblick der Tafel versagt oder ungenau erscheint. Insofern nun aber diese empirische Bestimmung des wahrscheinlichsten Wertes mit jener theoretischen übereinstimmen soll, müssen dem D alle die Eigenschaften beigelegt werden, die den Maximalwert des Verteilungsgesetzes auszeichnen, so daß einesteils die Berechnung des D durch Interpolation ein Mittel bietet, die Triftigkeit eines aufgestellten Verteilungsgesetzes zu erhärten, anderenteils, vor Kenntnis des aufzustellenden Gesetzes, die Erkenntnis der Eigenschaften des empirisch konstatierten D der Tafeln Fingerzeige zur Auffindung eines Verteilungsgesetzes geben kann.]

    § 41. [Dieser solidarische Zusammenhang zwischen den Eigenschaften des dichtesten Wertes D und dem Verteilungsgesetze, der dem D den unbedingten Vorrang vor jedem anderen Hauptwerte sichert, tritt auch in der physikalischen und astronomischen Fehlertheorie zu Tage. Dieselbe betrachtet bekanntlich als den wahren Beobachtungswert das arithmetische Mittel der beobachteten Werte, deren Abweichungen von jenem die Beobachtungsfehler sind. Der wahre Wert ist aber nichts anderes als der wahrscheinlichste Wert, der in einer Fehlerreihe, die hinreichend groß ist, um einen gesetzmäßigen Gang erkennen zu lassen, als empirisch dichtester Wert sich zu erkennen gibt. Es wird also durch Aufstellen des Prinzips, daß der wahre oder wahrscheinlichste Wert das arithmetische Mittel A sei, dem A die Bedeutung zugelegt, zugleich der dichteste Wert D zu sein. Diese Forderung des prinzipiellen Zusammenfallens von A und D führt nun zum GAUSS’schen Fehlergesetz, wie das z. B. aus ENCKE’s 1) Darstellung der Methode der kleinsten Quadrate zu ersehen ist. Auf Grund desselben folgt dann weiterhin auch die prinzipielle Übereinstimmung des Zentralwertes C mit A und mit D, deren vereinigte Lage für den Gang der Tafel Symmetrie bez. A bedingt, während ihr Auseinanderweichen Asymmetrie zur Folge hat.]

    1) [Berliner astronomisches Jahrbuch für 1834, S. 264 fg.]

    [Jenes Prinzip muß natürlich durch die Erfahrung Bestätigung finden. Damit wird jedoch nicht verlangt, daß für Fehlerreihen, deren Ausdehnung in den Stand setzt, einen dichtesten Wert durch den unmittelbaren Anblick der Reihe oder durch interpolationsmäßige Berechnung anzugeben, derselbe genau mit A zusammenfalle; denn man wird stets auf unausgeglichene Zufälligkeiten Rücksicht zu nehmen haben, die ein empirisches Auseinanderweichen der Hauptwerte verursachen können, ohne zugleich die Gültigkeit des aufgestellten Prinzips in Frage zu stellen. Überdies wird man eine Bewährung des Prinzips vielmehr in der Übereinstimmung des in der Fehlerreihe tatsächlich vorliegenden Ganges der Werte mit dem durch das Gesetz geforderten Gange, als in dem empirischen Zusammenfallen von A und D suchen und finden; wie denn auch z. B. BESSEL in den "Fundamenta astronomiae" durch Gegenüberstellen des Ganges der Fehler nach der Theorie und nach der Erfahrung eine Bewährung des G. G. gegeben hat. Es werden nämlich die unausgeglichenen Zufälligkeiten, insbesondere bei hinreichender Reduktion der Fehlertabelle, den Gang der Tafelwerte im ganzen wenig beeinflussen, während zu erwarten ist, daß sie die Lage einzelner Werte mitunter erbeblich stören und leicht ein verhältnismäßig beträchtliches Auseinanderweichen der Hauptwerte, deren Zusammenfallen von der Theorie verlangt wird, verursachen können.]

    Insofern aber ein solches Auseinanderweichen stattfindet, behält das arithmetische Mittel den Vorzug, sei es, daß man nach GAUSS’schen Prinzipien als den wahrscheinlichsten Wert denjenigen ansieht, bezüglich dessen die Summe der Abweichungsquadrate die kleinstmögliche ist, oder bezüglich dessen die Summe der Abweichungen nach beiden Seiten gleich ist; beide Werte aber fallen im arithmetischen Mittel zusammen, mag Symmetrie oder Asymmetrie bezüglich desselben stattfinden. Also bleibt der Vorzug für das arithmetische Mittel auch da, wo es nicht mit den anderen Hauptwerten zusammenfällt, in der physikalischen und astronomischen Maßlehre nach den Zwecken derselben jedenfalls entschieden.

    [Dies gilt jedoch nur unter der Voraussetzung, daß prinzipiell das arithmetische Mittel als der wahrscheinlichste Wert zu betrachten sei. Verliert dieses Prinzip seine Geltung, so verliert auch A seine bevorzugte Stellung; denn es behält zwar seine ursprüngliche Bedeutung als Durchschnittswert, aber mit Rücksicht auf das Verteilungsgesetz tritt jetzt derjenige Wert an seine Stelle, der dem nunmehr aufzustellenden Prinzipe gemäß die Rolle des wahrscheinlichsten Wertes übernimmt und prinzipiell mit dem dichtesten Werte zusammenfällt. Wird beispielsweise der Zentralwert C oder ein anderer "Potenzmittelwert", bezüglich deren Aufstellung und Erörterung auf die Abhandlung2): "Über den Ausgangswert der kleinsten Abweichungssumme" zu verweisen ist, als der Wert angesehen, dem die größte W. zukommen soll, so tritt im Zusammenhange damit jedesmal ein anderes Verteilungsgesetz in Kraft, durch dessen Bestehen der zu Grunde gelegte wahrscheinlichste Wert ganz ebenso die Vorherrschaft erhält wie bei Geltung des G. G. das arithmetische Mittel.]
 

    2) Abhandlungen der math.-phys. Klasse der Königl. Sächs. Gesellsch. der Wissensch. Band XI, 1878. (Insbesondere Abschnitt VI: "Bemerkungen zur Gültigkeitsfrage des Prinzips des arithmetischen Mittels" und Abschnitt VII: "Wahrscheinlichkeitsgesetze der Abweichungen bez. der verschiedenen Potenzmittel unter Voraussetzung der Gültigkeit ihres Prinzips.")
 

    § 42. [Für die Kollektivmaßlehre ist nun in gleicher Weise der dichteste Wert von fundamentalem Interesse, sobald das die Verteilung der Exemplare eines K.-G. beherrschende Wahrscheinlichkeitsgesetz in Frage kommt. Betreffs der Feststellung der Eigenschaften des dichtesten Wertes und der auf dieselben zu gründenden Ableitung jenes Gesetzes kann aber hier nicht das Prinzip des arithmetischen Mittels oder irgend ein anderes Prinzip a priori aufgestellt werden. Denn die K.-G. sind nur durch die Erfahrung gegeben, und es besteht von vornherein nicht einmal Sicherheit darüber, daß für dieselben insgesamt ein bestimmter Wert als wahrscheinlichster Wert zu finden ist, oder daß – mit anderen Worten – der empirisch dichteste Wert bei den verschiedenen K.-G. durch die nämlichen Eigenschaften charakterisiert werden kann. Es ist darum als ein grundlegendes Resultat der Erfahrung anzusehen, daß die verschiedensten K.-G., die in Untersuchung genommen wurden, in der Tat die Bestimmung eines wahrscheinlichsten Wertes gestatten, und daß der letztere nahe genug mit demjenigen Werte zusammentrifft, für den das Verhältnis der beiderseitigen mittleren Abweichungen (e' : e,) gleich ist dem Verhältnisse der beiderseitigen Abweichungszahlen (m' : m,). Der dichteste Wert ist somit in der Kollektivmaßlehre von dem arithmetischen Mittel prinzipiell verschieden und steht vielmehr in prinzipiell geforderter Übereinstimmung mit dem durch die Proportion e' : e,= m' : m,definierten Werte. Der letztere (welcher nach der in Kap. II getroffenen Festsetzung mit Dp zu bezeichnen ist, während Di den interpolationsmäßig berechneten, empirisch dichtesten Tafelwert benennt) beansprucht mithin hier die nämliche Beachtung wie der arithmetische Mittelwert in der Fehlertheorie. Auch hat er die ganz entsprechende Bedeutung; denn auf Grund des Prinzips, daß der wahrscheinlichste Wert eines K.-G. die Proportion e' : e, = m' : m, erfüllen, oder daß Dp = Di sein soll, findet man als Verteilungsgesetz das im vorigen Kapitel bereits vorgreiflich aufgestellte erweiterte G. G. in ähnlicher Weise, wie auf Grund des Prinzips, daß der wahrscheinlichste Wert das arithmetische Mittel, oder daß A = Di sein soll, das einfache G. G. als Fehlergesetz sich ergibt.]

    [Nur insofern kann A auch hier die Vorherrschaft behaupten, als es bei den mit schwacher Asymmetrie begabten K.-G. so nahe mit Dp zusammenfällt, daß es genügt, approximativ das einfache G. G. an Stelle des zweispaltigen in Anwendung zu bringen.]

    § 43. Nicht unberücksichtigt darf bei der Wahl zwischen den verschiedenen Hauptwerten der Grad der Leichtigkeit und Bestimmtheit bleiben, mit dem sie zu gewinnen sind. Kommt es auf bloß rohe Bestimmung an, so ist die des dichtesten Wertes entschieden die einfachste und leichteste, da man ja in einer Verteilungstafel bloß nach dem a zu sehen braucht, welchem das größte z zugehört; demnächst folgt in dieser Hinsicht die Bestimmung des Zentralwertes, wozu es nur einer Abzählung der a oder Q von beiden Seiten nach der Mitte bis zur erlangten Gleichheit von m¢ und m,bedarf; am umständlichsten die des A, da die Addition aller einzelnen a einer vielzahligen Verteilungstafel oder, was auf dasselbe herauskommt, die Bildung und Addition der Produkte za zur Erlangung der Summe åa, welche mit m zu dividieren ist, eine bei großem m langwierige und mühsame Operation ist.

    Aber anders, ja gerade umgekehrt, stellt sich das Verhältnis, wenn man zu scharfen, den idealen sich möglichst nähernden Bestimmungen übergehen will. Von der rohen Bestimmung des dichtesten Wertes nach dem auf ihn fallenden Maximal-z ist überhaupt nur eine sehr unsichere Approximation an den Idealwert zu erwarten; die schärfstmögliche aber, auf das Verhältnis m' : m, = e¢ : e,zu gründende, ist zwar auf eine bestimmte und nicht schwierig zu führende Rechnung zu bringen, aber wird in der Ausführung unstreng, fordert Reduktion und Interpolation, die zuletzt noch einen kleinen Spielraum für das zu rechnende Resultat lassen. Auch die scharfe Bestimmung des C, obwohl viel einfacher als die des D, kann ohne solche Hilfsmittel nicht auskommen, wogegen die Bestimmung des A solcher nicht bedarf. Die Umständlichkeit der Bildung der Produkte za kann durch ein später (Kap. IX) anzugebendes Verfahren vermieden werden.

    § 44. Nach voriger Besprechung der Eigenschaften und Leistungen der verschiedenen Hauptwerte wird noch etwas von den Gesichtspunkten zu sagen sein, aus denen die Extreme und Abweichungsfunktionen in Rücksicht kommen.

    Es können zwei K.-G. ganz oder nahe in ihren Hauptwerten übereinstimmen und doch noch die Schwankungsweite und der mittlere Schwankungswert der Exemplare um ihre Hauptwerte sehr verschieden sein, worin keineswegs gleichgültige Unterscheidungsmerkmale liegen. So kann die Mitteltemperatur einer Insel mitten im Ozeane und einer Örtlichkeit mitten in einem Kontinente dieselbe sein; aber die Abweichungen der einzelnen Temperaturen von der Mitteltemperatur halten sich bei der ersten in engeren Grenzen und sind im Durchschnitte kleiner als bei der zweiten, wonach wir Seeklima und Kontinentalklima unterscheiden.

    [Man wird nun geneigt sein, derartige Unterschiede durch Angabe des größten und des kleinsten Wertes, d. i. des E' und des E,, die in einer Reihe von Exemplaren eines K.-G. vorkommen, in einfachster Weise zu charakterisieren.]

    So empfehlenswert aber die Angabe der extremen Werte E' und E,ist, um erkennen zu lassen, in welchen Grenzen die Größe der Exemplare geschwankt hat, so ist doch der Nutzen davon aus mehr als einer Beziehung prekär und beschränkt. Einmal unterliegen diese Werte großen Zufälligkeiten, so daß man nicht darauf rechnen kann, wenn man die Extreme und extreme Schwankung aus einer neuen Serie von Exemplaren mit demselben m bestimmt, dieselben Werte wieder zu finden; zweitens hat die Angabe derselben überhaupt nur für die Anzahl der Exemplare, das m , woraus dieselben abgeleitet sind, einen Wert, indem bei größerem m der Spielraum der Veränderungen größer wird, so daß man bei größerem m im allgemeinen weiter auseinanderliegende Extreme, ein kleineres E,, ein größeres E' und mithin eine größere extreme Schwankung E' - E,erhält als bei kleinerem m . Gesetzt nun z. B. man will einen Maßstab für die absolute und relative Veränderlichkeit eines K.-G. in dem Werte E' - E, oder (E' - E,) : A suchen, wie es wohl geschieht, und danach verschiedene K.- G. vergleichen, so wird man die größten Irrtümer begehen, wenn die Gegenstände ein verschiedenes m haben, und ich bin Irrtümern dieser Art, die auch zu irrigen Folgerungen führten, wirklich anderwärts begegnet.3)
 
 

    3) [Dieser Absatz ist einem Exposé FECHNER’s über mittlere Abweichungen und Extreme entnommen, das im Jahre 1868 Herrn Prof. WELCKER mitgeteilt und von diesem mir zur Verfügung gestellt wurde.]
 

    Besser als die Schwankungsweite E' - E,eignet sich daher die mittlere Schwankung, identisch mit mittlerer Abweichung, zum Maße der Veränderlichkeit eines Gegenstandes, da sie ziemlich unabhängig von m ist und durch eine geeignete Korrektion vollends unabhängig davon gemacht werden kann. Allerdings ändert sich dies Maß nach dem Hauptwerte, von dem man die Abweichungen rechnen will, und ist, allgemein gesprochen, für positive und negative Seite verschieden. Der Berücksichtigung letzterer Verschiedenheit aber entgeht man, wenn man überall die Totalsumme der Abweichungen nach beiden Seiten, dividiert mit der Totalzahl der Abweichungen nach beiden Seiten, dazu verwendet, also nach unserer allgemeinen Bezeichnung als mittlere Schwankung oder mittlere Abweichung schlechthin bezüglich eines gegebenen Hauptwertes setzt:

.

Ob man dazu die Abweichungen des einen oder anderen Hauptwertes verwenden will, kommt darauf an, auf welchen man sich überhaupt beziehen will, und eins schließt das andere nicht aus. Wie man sieht, ändert sich das Maß bei gegebenem m nach der Totalsumme der beiderseitigen Abweichungen bezüglich der verschiedenen Hauptwerte; bis jetzt hat man bloß von den Abweichungen des arithmetischen Mittels Gebrauch gemacht, und bleiben wir zunächst dabei stehen, so erhalten wir als mittleren Schwankungswert im Sinne obiger Bezeichnung:

.

    Nun ist allerdings h nicht ganz unabhängig von der Größe des m , sondern es verhält sich so: Der Wert A, von dem die Abweichungen genommen werden, ändert sich etwas je nach der Zahl der a , mithin des m derselben, woraus er das Mittel bildet; und das genauest mögliche A könnte nur aus einem unendlichen m erhalten werden. Mit der Größe des endlichen m, also jedenfalls ungenauen A aber ändert sich auch die Größe der Abweichungen und mithin die Summe derselben, durch deren Division mit m der Wert h gewonnen wird, und zwar lehrt Theorie und Erfahrung4), daß å D und mithin h = åD : m bei wachsendem m durchschnittlich im Verhältnisse wächst, wonach man å D , sowie h auf den Normalfall, daß die Bestimmung des A mit seinen Abweichungen aus einem unendlichen m geschehen wäre, zurückführen kann, indem man åD resp. h mit , merklich = 2 m : (2 m - 1), multipliziert, was man die Korrektion wegen des endlichen m nennt. Das so korrigierte h heiße hc , und findet sich also:

.






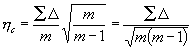    4) In beider Hinsicht vergl. meine Abhandlung in den Berichten der Königl. Sächsischen Gesellschaft der Wissenschaften, Band XIII, 1861 ["Über die Korrektionen bezüglich der Genauigkeitsbestimmung der Beobach-tungen, der Bestimmung der Schwankung meteorologischer Einzelwerte um ihren Mittelwert und der psycho-physischen Maßbestimmungen nach der Methode der mittleren Fehler"].
 
 

    Diese Korrektion trifft zwar nicht in jedem einzelnen Falle, aber im Durchschnitte der Fälle zu, und da man kein Mittel hat, sie für jeden einzelnen Fall zutreffend genau zu bestimmen, muß man sich an den Wert halten, der doch im Durchschnitte der Fälle zutrifft, und kann sich also, wenn man die kleine Mühe der Korrektion nicht scheut, auch in der Kollektivmaßlehre lieber an hcals an h halten.

    Soll die mittlere Schwankung bezüglich C oder D bestimmt werden, so hat man ohne Korrektion erstenfalls e = åQ: m , zweitenfalls e = å¶ : m , die Korrektion aber würde, so viel ich übersehe, dieselbe bleiben. Die mittlere Schwankung bezüglich C hat das Interesse, daß sie kleiner als bezüglich A und D , überhaupt die kleinstmögliche ist, weil nach schon früher gemachter Angabe die Summe der Abweichungen bezüglich C überhaupt die kleinstmögliche ist, und dies sich auf ihren Quotienten durch m überträgt.

    Allgemein gesprochen, obwohl dies Ausnahmen erleiden kann, und eine genaue Proportionalität nicht statt findet, wächst die mittlere Schwankung mit der Größe der Gegenstände, und so kann es von Interesse sein, diesen Einfluß so weit als möglich dadurch zu eliminieren, daß man die mittlere Schwankung durch die Größe des schwankenden Gegenstandes dividiert, hiermit das relative außer dem absoluten Schwankungsmittel in Betracht zieht.

    § 45. Eine wichtigere Bedeutung als zum Maße der Schwankung eines Gegenstandes um seine Hauptwerte gewinnt die mittlere Abweichung als Mittelglied für Bestimmung der Verteilung des Gegenstandes. Die physikalische und astronomische Maßlehre macht zu diesem Zwecke von der mittleren Abweichung ebezüglich A oder dem zu ein Beziehung stehenden Werte  Gebrauch, was aber nur für die in dieser Lehre vorausgesetzte symmetrische W. der Beobachtungsfehler zulässig ist, wogegen die Kollektivmaßlehre nach der für sie tatsächlich bestehenden allgemeineren Voraussetzung der Asymmetrie nur von der mittleren Abweichung bezüglich D, und zwar nicht gemeinschaftlich für beide Seiten, sondern jede Seite insbesondere Gebrauch machen kann (vergl. § 33), also von:

.

    Auch hierbei ist streng genommen eine Korrektion wegen des endlichen m anzubringen; aber die korrigierten Werte sind nicht, wie man meinen könnte, zu setzen:

, ,

sondern:

, 

    In der Tat würde sonst die auf die Abweichungssummen bezügliche Korrektion der beiden Seiten nicht mit der gemeinsamen Korrektion der Totalsumme derselben stimmen.

    Für die Totalsumme hat man nämlich:

.

Wollte man nun für die beiderseitigen Abweichungssummen besonders setzen:

, ,

so würde man durch Summierung dieser Werte erhalten:

,

was mit obigem Werte für å¶c nicht stimmt.

    § 46. Endlich ist noch einiger Werte zu gedenken, welche zu den schon wiederholt berührten, doch erst später eingehend zu besprechenden, sehr wichtigen Asymmetrieregeln in Beziehung stehen. Vorläufig nur folgendes über diese Werte.

    Es ist zunächst der Unterschied µ' - µ,= u zwischen der Zahl der positiven und negativen Abweichungen von A und der Unterschied U¢- U, = (E¢- A) - (A - E,) = E' + E,-2A zwischen der Größe der positiven und negativen extremen Abweichung von A, welche in dieser Hinsicht in Betracht kommen. Noch wichtiger aber als diese absoluten Unterschiede sind die relativen:

und .

Hier nur vorläufig in Rücksicht auf den später davon zu machenden Gebrauch folgendes darüber.

    Von einem Unterschied zwischen der Summe der positiven und negativen Abweichungen von A , d. i. åD ' und åD,, kann natürlich nicht die Rede sein, da ja A ausdrücklich so bestimmt wird, daß beide Summen gleich werden; aber das führt noch nicht mit, daß zugleich beide Abweichungszahlen µ' , µ,einander gleich werden, und höchstens zufällig wird man es einmal finden. Was man aber allgemein oder nur mit zufälliger Ausnahme, jedenfalls im Durchschnitt bei den Kollektivabweichungen bezüglich A findet, ist, daß µ' - µ,mit der Größe von m wächst.

    Unter Voraussetzung gleicher W. positiver und negativer Abweichungen lehrt nämlich die Wahrscheinlichkeitsrechnung nach Zurückführung des Falles auf die Urne mit der gleichen Zahl schwarzer und weißer Kugeln, daß µ¢ - µ,seinem absoluten Werte nach durchschnittlich im Verhältnisse von  steigt. Je mehr aber m steigt, desto kleiner wird das Verhältnis von : m, so daß, bei unendlichem m ,  Null und Eins wird.

    Eine Folge daraus ist, daß man bei der später folgenden Untersuchung, ob die positiven und. negativen Abweichungen bez. A wirklich eine gleiche W. haben, sich nicht einfach an den absoluten Unterschied u halten darf, der im allgemeinen auch bei gleicher W. nicht fehlt, sondern an sein Verhältnis zu m , das eine gewisse Größe nicht übersteigen darf, soll die gleicheW. nicht sehr unwahrscheinlich werden, worüber später mehr zu sagen sein wird.

    Bisher haben wir die Ungleichheit der beiderseitigen Zahl der Abweichungen bez. A d. i. µ' , µ,als Merkmal und in gewisser Rücksicht als Maßstab der Asymmetrie angenommen. Natürlich könnte von einer Asymmetrie wegen Ungleichheit der Abweichungssumme åD ', åD,bez. A nicht die Rede sein, weil es im Begriffe von A liegt, daß åD ' = åD,, also A so bestimmt werden muß, daß diese Gleichheit eintritt; andererseits könnte auch ein Merkmal oder Maßstab der Asymmetrie nicht auf eine Ungleichheit der Zahl der Abweichungen bez. C gegründet werden, weil es im Begriffe von C liegt, daß die beiderseitige Zahl der Abweichungen in Beziehung dazu gleich ist; hiergegen würde an sich nichts hindern, die Asymmetrie statt in Bezug auf den arithmetischen Mittelwert A auf den dichtesten Wert D nach der Ungleichheit der Abweichungszahlen m¢, m,zu bestimmen, im Falle beide Hauptwerte genügend aus einander weichen; mit dem Vorteil, in Bezug auf D ein in den Gesetzen der Asymmetrie begründetes stärkeres Auseinanderweichen der Abweichungen m¢, m,von einander, als der Abweichungen µ' , µ, bez. A von einander zu erhalten; und die m' , m,mit dem zweiseitigen G. G, in Beziehung setzen zu können, während bei stattfindender Asymmetrie gegen A weder das einfache, noch zweiseitige G. G. bezüglich der Abweichungszahl von A mehr gültig ist. Wobei zu beachten, dass, wenn bez. A µ¢über µ,übergreift, umgekehrt m,über m¢ übergreift. Da aber A und hiernach µ' , µ,viel leichter zu bestimmen sind als D und hiernach m' ,m,, und von einer größeren oder geringeren Asymmetrie bez. A immer auf eine größere oder geringere, nur in jedem Falle die Asymmetrie bez. A übersteigende Ungleichheit bez. D von entgegengesetzter Richtung geschlossen werden kann, so erscheint es im allgemeinen praktischer, sich zunächst an die Ergebnisse der Bestimmung der Asymmetrie durch µ¢ - µ,bez. A zu halten, insofern daraus schon auf die Ungleichheit von m¢ und m, bez. D geschlossen werden kann; sofern es aber um genaue Bestimmung zu tun, ist diese noch besonders nach Theorie und Empirie zu untersuchen.