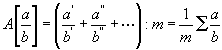 . (1)
. (1)Bemerktermaßen können nicht bloß einfache Dimensionen eines Gegenstandes, sondern auch Verhältnisse derselben kollektiv behandelt werden, und schon oben (Kap. I und III) erwähnte ich in dieser Hinsicht die Verhältnisse zwischen den Schädeldimensionen einer gegebenen Rasse und den Stengelabteilungen, sog. Gliedern oder Internodien einer Graminee, wozu sich genug andere Beispiele finden lassen. Halten wir uns an das Verhältnis zwischen der vertikalen Dimension a und der zugehörigen horizontalen b des Schädels einer gegebenen Rasse, was zum Vergleiche mit anderen Rassen bestimmt werden soll, und setzen dabei in der Regel a in den Zähler, b in den Nenner, obwohl das Verhältnis ebenso gut umgekehrt genommen werden kann. Das Verhältnis a : b ist nun schon zwischen den Exemplaren einer und derselben Rasse etwas verschieden; aber zur vergleichenden Charakteristik anderen Rassen gegenüber gehören statt der wechselvollen Einzelbestimmungen einheitliche Resultate daraus. Man kann daher nur ein mittleres Verhältnis zwischen b und a verlangen, was im allgemeinen mit M [a : b] bezeichnet wird. Jenachdem man das arithmetische oder geometrische Mittel im Auge hat, treten A oder G an die Stelle von M . Die entsprechende Aufgabe kann bezüglich der zu einander gehörigen Dimensionen desselben Teiles oder derselben Dimensionen an verschiedenen Teilen nicht nur des Menschen, sondern irgend welchen Gegenstandes aufgestellt werden. So kann man fragen, wie verhält sich im Mittel die Länge des einen Fingers zu der des anderen, die Länge des einen Gliedes zur Länge des zweiten Gliedes einer Ähre, die Länge zur Breite einer Visitenkarte, die Mitteltemperatur eines Monats zu der eines anderen u. s. w., kurz, dieselbe Aufgabe bietet sich unendlich oft dar.
§ 148. Ein mittleres Verhältnis kann nun aber auf verschiedene Weise gewonnen werden; namentlich auf folgende, wobei zu einander gehörige Werte von a und b mit gleichem Index bezeichnet werden sollen. Die für die Richtung a : b aufgestellten Beispiele können natürlich für die Richtung b : a umgesetzt werden.
1) Das arithmetische Mittel von Verhältnissen A [a : b] wird dadurch erhalten, daß man alle Einzelwerte a : b addiert und mit der Zahl derselben dividiert; also:
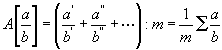 . (1)
. (1)![]() . (2)
. (2)
Man könnte gegen die Anwendung dieses Mittels geltend machen, es sei vielmehr ein Verhältnis zwischen Mitteln als ein Mittel aus Verhältnissen; aber indem es das eine ist, ist es zugleich das andere in dem weiteren Begriffe des Mittels, den wir hier überhaupt gebrauchen, sofern es nach einem bestimmten Prinzip zwischen die Einzelwerte von a : b und zwar, abgesehen von ganz exzeptionellen Fällen, in die Nähe der anderen Mittel fällt.
3) Prozentisches Mittel. Zur Gewinnung dieses Mittels bildet man die Werte a : (a + b) und b : (a + b) und dividiert die Summe der einen durch die der anderen nach der Formel:
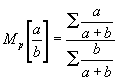 .
(3)
.
(3)
4) Das geometrische Mittel, repräsentiert durch die Formel:
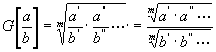 ,
(4)
,
(4)
ist das geometrische Mittel aus dem Produkt der einzelnen Verhältnisse a : b oder, gleichgeltend damit, das geometrische Mittel aus dem Produkte der a , dividiert durch das der b , und wird in praktischem Wege als der in den Logarithmentafeln gesuchte Zahlwert zu (å log a - ålog b) : m erhalten.
Fragt man nun nach der Wahl zwischen diesen verschiedenen Mittelbestimmungen, so ist zuvörderst im allgemeinen ebenso wie bezüglich der einfachen Maße vorzubemerken, daß, insofern es sich nur um eine Charakteristik der Verhältnisse eines K.-G. handeln sollte, welche einen Vergleich desselben mit anderen Gegenständen gestattet, jedes der angeführten Mittel nur aus einem anderen Gesichtspunkte zu einer solchen Charakteristik beiträgt, und daß, wo das Verhältnis a : b überhaupt nur verhältnismäßig wenig schwankt, alle vier Bestimmungsweisen fast auf denselben Wert führen. So gaben z. B. 10 Visitenkarten, nach Zufall aus einem Paket herausgezogen, wenn die kurze Seite mit a , die lange mit b bezeichnet wird, als Mittel:
arithmetisch 0,5654
summarisch 0,5634
prozentisch 0,5650
geometrisch 0,5649.
Die extremen Werte a : b waren 0,5333 und 0,6053.
Inzwischen, wo die Schwankungen zwischen den a : b bedeutend sind, können auch die verschiedenen Mittelbestimmungen ein erheblich verschiedenes Resultat geben, und überhaupt gilt es, die Gesichtspunkte anzugeben, welche die Wahl der einen Bestimmungsweise vor der anderen entscheiden können.
In dieser Hinsicht kann man allgemein sagen, daß das arithmetische und prozentische Mittel in jeder Beziehung den beiden anderen Mittelwerten nachstehen und allgemein gesprochen das geometrische Mittel den Vorzug verdienen dürfte, aber auch das summarische unter Umständen eine nützliche Verwendung finden kann.
In der Tat leidet zunächst das arithmetische Mittel von Verhältnissen an folgenden Nachteilen.
a) Um die einzelnen Brüche a : b addieren zu können, muß man erst jeden einzelnen auf einen Dezimalbruch reduzieren, was bei vielen Werten a : b sehr mühsam ist.
b) An sich ist es gleichgültig, ob man die direkten Werte a : b oder die reziproken Werte b : a zur Mittelziehung benutzen will, um das mittlere Verhältnis der a und b zu bestimmen; und man sollte natürlich auf beiden Wegen ein übereinstimmendes Resultat erlangen; dies gewährt aber diese Methode nicht, wie sich zeigt, wenn man das aus den reziproken Werten gewonnene Mittel umkehrt, wodurch man das sog. harmonische Mittel zu dem aus den direkten Werten gewonnenen erhält; beide stimmen nicht überein, kurz A [a : b] ist nicht gleich dem dazu harmonischen Mittel 1 : A [b : a]. Sei z. B., um ein ganz einfaches Beispiel von nur zwei Verhältnissen zu nehmen:
![]() ;
; ![]() ;
;
so ist:
c) Hat man die mittleren Verhältnisse zwischen dreierlei Werten a , b , c zu bestimmen, so sind drei Verhältnisse a : b , b : c , a : c mit ihren reziproken Werten möglich, und man kann wünschen, aus zweien dieser Verhältnisse (sei es direkter oder reziproker) unmittelbar das dritte ableiten zu können. Dies leistet aber diese Methode nicht, indem man z. B. A [a : c] nicht dadurch erhalten kann, daß man A [a : b] mit A [b : c] multipliziert.
Das prozentische Mittel teilt diese sämtlichen Nachteile des arithmetischen. Doch findet man mitunter sowohl das eine wie das andere gebraucht.
Das summarische und geometrische Mittel
sind hingegen frei von diesen sämtlichen Nachteilen. Wollte man aber
doch dem direkten arithmetischen und prinzipiell gleichberechtigten harmonischen,
aber vom direkten verschiedenen Mittel ein besonderes Zutrauen schenken,
so würde man sich nur an das arithmetische oder geometrische Mittel
des direkten und harmonischen Mittelwertes halten können. Aber da
es ja auch freistände, statt von a : b , von
b
: a als direktem Verhältnis auszugehen, so würde
nicht nur hierdurch eine Zweideutigkeit bleiben, sondern auch bei Wahl
des arithmetischen Mittels wieder die Frage entstehen, ob man das direkte
oder harmonische vorziehen sollte, also die Zweideutigkeit auch von dieser
Seite nicht gehoben sein. Nach einem Beweise aber, den ich Prof. SCHEIBNER
1) verdanke, fällt der geometrische
Mittelwert gegebener Verhältnisse in dem bei K.-G. in der Regel stattfindenden
Falle, daß das direkte und harmonische arithmetische Mittel sich
wenig unterscheiden, merklich genau mit dem arithmetischen Mittel beider
zusammen, und man kann dies an selbst gemachten Beispielen leicht bestätigt
finden.
1) [Vergl. W. SCHEIBNER: "Über Mittelwerte",
Berichte der Kgl. Sächsischen Gesellschaft der Wissen-schaften. 1873.
S. 564. – Nach den dort gegebenen Bestimmungen ist das geometrische Mittel
angenähert gleich: 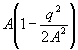 ,
,
das harmonische Mittel gleich: 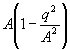 ,
,
wenn A das arithmetische Mittel und q den mittleren quadratischen
Fehler bedeutet; woraus der obige Satz folgt.]
§ 149. Schließlich also dürfte es sich nur um die Frage, wiefern das summarische oder geometrische Mittel vorzuziehen, handeln.
Nun empfiehlt sich das summarische Mittel vor allem durch die Leichtigkeit seiner Bestimmung, da es dazu nur der Summierung aller a , sowie aller b und der Division der einen Summe durch die andere bedarf, indes es zur Gewinnung des geometrischen Mittels gilt, erst alle a und b in Logarithmen zu übersetzen. Beide haben aber folgenden prinzipiellen Unterschied in der Bedeutung.
Sei ein summarisches Mittel:
gegeben, so leuchtet ein, daß wenn etwa ein Exemplar nach seinen beiden in das Verhältnis eingehenden Komponenten a' und b' sehr groß gegen die übrigen wäre, das Mittelverhältnis merklich bloß noch von dem Verhältnis a' : b' abhängen würde, indem dann a" + a"' + × ×× gegen a' und b" + b"' + × ×× gegen b¢ verschwinden, und daß überhaupt die größeren Exemplare nach Maßgabe ihrer Größe auch mehr Einfluß auf das Mittel gewinnen. Dies ist nun ganz in der Ordnung, wenn man größeren Exemplaren mehr Gewicht für die Mittelbestimmung beilegt als kleineren, was unter Umständen sehr wohl der Fall sein kann, und jedenfalls hindert nichts in dem summarischen Mittel, was diesen Umstand mitführt, so gut ein charakteristisches Verhältnis des gegebenen K.-G. zu sehen, als in jedem anderen Mittelverhältnis, was ihn nicht mitführt, indem es den Gegenstand nur eben in anderem Sinne charakterisiert.
Hingegen kann es freilich auch in der Absicht liegen, große und kleine Exemplare mit gleicher Wichtigkeit zur Mittelbestimmung beitragen zu lassen, z. B. das Verhältnis zwischen horizontaler und vertikaler Dimension bei größeren Köpfen nicht wichtiger zu nehmen als bei kleineren, und dieser doch wohl häufiger vorkommenden Absicht entspricht das geometrische Mittel.
Den dem arithmetischen und prozentischen Mittel abgehenden Vorteil, daß, wenn von drei Verhältnissen a : b , b : c , a : c zwei im Mittel bestimmt sind, das Mittel des dritten unmittelbar daraus folgt, teilt das summarische Mittel mit dem geometrischen, indem man nach beiden hat:
![]() .
(5)
.
(5)
Hingegen hat das summarische Mittel folgenden Vorteil vor dem geometrischen voraus. Gesetzt, man hat bei einem mehrgliedrigen Gegenstande, z. B. Getreidehalmen gegebener Art, für jedes Glied insbesondere das mittlere Verhältnis seiner Länge zur Totallänge des Halmes summarisch bestimmt, so braucht man diese Verhältnisse nur für irgend welche zwei Glieder zu addieren, um damit das mittlere Verhältnis der Verbindung dieser zwei Glieder zur Totallänge zu haben, was beim geometrischen Verfahren nicht der Fall ist, wie man leicht beweist; was man kurz so ausdrücken kann: die Verhältnismittelbestimmungen für die Teile und das Ganze hängen nach dem summarischen Verfahren rationeller zusammen als nach dem geometrischen und überhaupt jedem anderen.
Außerdem ist folgender Fall zu berücksichtigen. Setzen wir, bei einem K.-G. kommen unter anderen Exemplare vor, für welche der eine oder andere von beiden Werten a oder b Null ist; wie denn z. B. bei Bestimmung des mittleren Verhältnisses zwischen den Gewichten der festen und weichen Teile verschiedener Tiere manchen feste Teile ganz abgehen können. In diesem Falle wird das geometrische Mittel unbrauchbar, weil, je nachdem der Nullwert im Zähler oder Nenner auftritt, das Mittel Null oder unendlich wird. Dann kann man sich doch nur an das summarische Mittel halten, wenn man nicht das Prinzip aufstellen will, daß solche Fälle überhaupt nicht mit solchen, wo a und b überall endliche Werte behalten, unter demselben Mittel zu vereinigen sind.
§ 150. Da jedenfalls der vorliegende Gegenstand durch das summarische und geometrische Verhältnis der Komponenten a und b , welche in seine Bestimmung eingehen, in verschiedener Weise bestimmt ist, so wird, allgemein gesprochen, zur Vollständigkeit seiner Bestimmung gehören, daß man beiderlei Mittel bestimmt, was nicht hindert, nach Maßgabe der Umstände doch lieber von dem einen vor dem anderen Gebrauch zu machen2). Es hat aber die Bestimmung von beiden außer dem allgemeinen Beitrag zur Charakteristik eines gegebenen K.- G., dessen Komponenten a und b sind, noch den Vorteil, daß mit dem Verhältnisse beider Mittel nicht unwichtige spezielle charakteristische Bestimmungen zusammengehören, nämlich folgende:
1) Wenn das Verhältnis von a zu b unabhängig von der absoluten Größe der a und b für alle Exemplare gleich ist, also für große Exemplare ebenso groß als für kleine, ist das sum-marische Mittel gleich dem geometrischen.
2) Wenn a mit b immer zugleich wächst oder abnimmt, aber nicht allgemein im gleichen Verhältnisse, so kann es sein, daß das Verhältnis a : b mit wachsender Größe von a und b zunimmt, oder daß es abnimmt; ersteres ist der Fall, wenn das geometrische Mittel der a : b kleiner ist als das summarische, letzteres, wenn es größer ist.
3) Wenn die verhältnismäßige Schwankung der Werte a um ihr arithmetisches Mittel A gleich der verhältnismäßigen Schwankung der Werte b um ihr arithmetisches Mittel B ist, so ist das geometrische Mittel gleich dem summarischen. Als Maß der verhältnismäßigen Schwankung gilt hierbei bez. A die einfache oder quadratische mittlere Abweichung von A , dividiert durch A , nämlich ea: A oder qa : A , sagen wir kurz P ; entsprechend eb: B oder qb : B , kurz Q , bezüglich B .
4) Je nachdem die verhältnismäßige Schwankung der Werte, im vorigen Sinne verstanden, stärker um A oder um B ist, ist das geometrische Mittel kleiner oder größer als das summarische.
5) Aus Kombination von 1) und 2) mit
3) und 4) folgt dann weiter noch, daß, je nachdem die verhältnismäßige
Schwankung um A gleich der um B , größer oder
kleiner ist, der Wert a : b unabhängig von dem
absoluten Werte der a und b konstant ist oder mit wachsender
Größe von a und b zunimmt oder abnimmt [vorausgesetzt,
daß überhaupt der Wert a : b ein reguläres
Verhalten zeigt und bloß zwischen Konstanz, ständiger Zunahme
und ständiger Abnahme eine Entscheidung zuläßt].
2) So gut man zwei oder mehrere K.-G.
nach dem Verhältnisse ihrer Mittel A und G vergleichen
kann, kann man sie natürlich auch nach dem Verhältnisse ihrer
C
und D vergleichen, und es geben sich diese sämt-lichen Resultate
keineswegs allgemein proportional; doch gehe ich auf allgemeine Erörterungen
hierüber nicht näher ein. – Beispielsweise war bei 237 deutschen
Männerschädeln das mittlere Verhältnis (Hor. : Vertik.)
des Vertikalumfanges der Schädelkapsel zum Horizontalumfang summarisch
1,2830; geometrisch 1,2827; zentral 1,2837.
Hiernach also kann man aus dem Verhältnisse des geometrischen zum summarischen Mittel, ohne eine weitere Rechnung anzustellen, unmittelbar Schlüsse ziehen, ob mit wachsender Größe eines Gegenstandes und hiermit seiner Komponenten a und b das Verhältnis a : b überall (oder doch vorwiegend) wächst oder abnimmt, und ob die eine oder andere Komponente a , b in stärkerem Verhältnisse um ihr arithmetisches Mittel schwankt.
Folgendes zum Beweis für vorstehende Sätze. Den ersten anlangend, so seien das summarische und geometrische Mittel:
![]()
allgemein zwischen a' : b' , a" : b", ... fällt. Sind nun a' : b' , a" : b", ... sämtlich gleich a: b, so wird das Zwischenfallen zur Gleichheit mit a : b , während nicht minder das geometrische Mittel sich für den Fall der Gleichheit zwischen a' : b¢, a" : b" , ... auf a : b reduziert. Nach Maßgabe aber als die Gleichheit zwischen den einzelnen Werten a : b aufhört, hört auch, allgemein gesprochen, die Gleichheit zwischen beiden Mitteln auf, und es kann nun sein, daß a : b mit Änderung der absoluten Größe von a und b teils zunimmt, teils abnimmt, für welchen Fall sich nichts Allgemeines festsetzen läßt. Gesetzt aber, a und b nehmen überall mit einander zugleich zu oder ab, ohne daß es doch überall in gleichem Verhältnisse geschieht, so gibt es für den Satz 2) einen allgemeinen Beweis, den ich Herrn Prof. SCHEIBNER verdanke, der jedoch umständlich und nicht elementar ist, daher ich hier vorziehe, auf die empirische Bewährung der Regel durch beliebige, selbst gemachte Beispiele zu verweisen. Und natürlich wird die Regel auch für den Fall noch gelten, wenn nur a und b in der Überzahl der Fälle mit einander zugleich zu- oder abnehmen. Den dritten und vierten Satz anlangend, so sind sie eine Folgerung des von SCHEIBNER3) gegebenen Verhältnisses zwischen arithmetischem und geometrischem Mittel der einfachen Werte. Hiernach hat man unter Setzung von P und Q als qa : A und qb : B :
![]() ;
; ![]()
![]() ; (6)
; (6)
woraus die Sätze 3) und 4) folgen. Sind nun schon
die betreffenden Formeln nur approximative, so wird doch durch die weggelassenen
kleinen Glieder die Richtung der Resultate nicht geändert. Der Satz
5) folgt aus den vorgängigen.
Es entsteht nämlich die Frage, ob ebenso wie die einzelnen Dimensionen a und b , auch ihre Verhältnisse a : b sich unseren Verteilungsgesetzen fügen; eine Untersuchung, bei der dann allerdings der Rückgang auf die einzelnen a : b nicht erspart werden kann, von vornherein aber nach den bisher gemachten Bemerkungen einleuchtet, daß man von einer arithmetischen Behandlung derselben nichts erwarten kann; wogegen Aussicht war, daß nach Aufsuchung des dichtesten Wertes der log (a : b) die Abweichungen der einzelnen log (a : b) von demselben sich unseren Verteilungsgesetzen fügen könnten, was sich bei den zur Untersuchung geeigneten K.-G. bestätigt gefunden hat.
[Um dies durch ein Beispiel zu illustrieren,
wähle ich das Verhältnis des Horizontalumfanges zum Vertikalumfange
(genauer Scheitelbogen) der 500 europäischen Männerschädel,
die mir von Prof. WELCKER zur Verfügung gestellt sind. Da der horizontale
Umfang durchweg größer ist als der vertikale – der kleinste
Horizontalumfang ( für einen Kleinrussen ) ist 465 mm ; der größte
Scheitelbogen ( für einen Schädel aus der Umgegend von Halle
) ist 448 mm – so sind die Verhältnisse sämtlich unechte Brüche
und ihre Logarithmen positiv. Das Minimum der Verhältniswerte ist
gleich 1,211 , das Maximum gleich 1,403 . Die logarithmischen Werte variieren
somit zwischen den Grenzen 0,083 und 0,147; sie besitzen den Mittelwert
G1
= 0,1073 , so daß das geometrische Mittel G1der
Verhältnisse gleich 1,280 ist. Wählt man nun als logarithmisches
Intervall i = 0,003 und als untere Grenze des ersten Intervalles
den Wert 0,0825 , so erhält man folgende Vergleichstabelle zwischen
den empirischen und den durch das logarithmische Verteilungsgesetz geforderten
theoretischen Werten:
Verhältnis des Horizontalumfanges a zum Vertikalumfange (Scheitelbogen) b für 500 europäische Männerschädel.
|
a |
|
|
| empir. | theor. | |
| — | — | 1 |
| 0,084 | l | 2 |
| 0,087 | 4 | 5 |
| 0,090 | 12 | 10 |
| 0,093 | 17 | 19 |
| 0,096 | 29 | 32 |
| 0,099 | 47 | 46 |
| 0,102 | 64 | 58,5 |
| 0,105 | 64 | 65 |
| 0,108 | 67 | 64 |
| 0,111 | 61 | 58 |
| 0,114 | 45 | 47 |
| 0,117 | 36 | 36 |
| 0,120 | 28 | 24,5 |
| 0,123 | 11 | 15 |
| 0,126 | 7 | 9 |
| 0,129 | 3 | 4,5 |
| 0,132 | 2 | 3 |
| 0,135 | 1 | 0,5 |
| 0,138 | 0 | — |
| 0,141 | 0 | — |
| 0,144 | 0 | — |
| 0,147 | 1 | — |
| Summe | 500 | 500 |
G2= 0,1073 G2 = 1,280
C = 0,1070 C = 1,279
Di = 0,1068 Ti= 1,279
Dp = 0,1060 Tp= 1,276
e' = 0,0079
e,= 0,0066
m' = 272,5
m,= 227,5
h' = 7142
h,= 85,48 .
Hierzu ist zu bemerken, daß Di nicht den aus der obigen Tabelle direkt ableitbaren, empirisch dichtesten Wert darstellt (der vielmehr gleich 0,1075 ist), sondern das Mittel der drei aus den drei möglichen Reduktionslagen berechneten Werte: 0,1075 ; 0,1085 ; 0,1043 . Diese Bestimmungsweise wurde gewählt, weil hier zufällig die Reduktionslage von großem Einflusse auf die Lage von Diist, während G2und C fast vollständig mit den aus der primären Tafel resultierenden Werten übereinstimmen. Die Asymmetrie ist schwach; wie denn auch
![]()
nahe mit ¼p =
0,785 übereinstimmt. Die Übereinstimmung zwischen den
empirischen und theoretischen z-Werten aber ist ohne Zweifel befriedigend.]