Von den folgenden 6 Versuchsreihen ist I bis IV insbesondere bestimmt, zu beweisen, daß das Weber’sche Gesetz sich für das Tastmaß nicht eben so wie für das Augenmaß bestätigt, sondern daß der mittlere Fehler oder die Fehlersumme, woraus er gezogen worden, sich in kleinerem Verhältnisse vergrößert, als die Normaldistanzen auf der Haut, bei denen er erhalten wird, und daß er bei größeren Distanzen fast konstant bleibt; die Reihe V, eine sehr große mit 6400 Beobachtungen, zeigt, daß die 5 Finger (Vorderglied, Volarseite, Längsdistanz) sich in dem Grade der Unterschiedsempfindlichkeit nicht sehr unterscheiden, der Zeigefinger aber doch entschieden die größte Empfindlichkeit besitzt, ein Resultat, das, um für allgemein zu gelten, freilich erst noch an anderen Personen konstatiert werden müßte, und bei verschiedener Gebrauchsweise der Hände zur Arbeit und den täglichen Verrichtungen des Lebens möglicherweise sich verschieden stellen könnte. Die Reihe VI gibt den Maximumgrad der Unterschiedsempfindlichkeit, den ich bis jetzt mit dem Tastorgane erlangte, worüber (Kap. 34) gesprochen worden ist.
Abgesehen hiervon sind die folgenden Reihen, besonders V und VI, bestimmt, die Methode der mittleren Fehler nach verschiedenen Seiten etwas spezieller an Beispielen zu erläutern. Hierbei wird ein Rückblick auf das vorausgesetzt, was in Th. I, Kap. 8, insbesondere von S. 120 an, über die Methode der mittleren Fehler gesagt ist, wozu noch die Bemerkungen in Th. II, Kap. 28 über die Analyse des konstanten Fehlers c in seine Komponenten zugezogen werden können, wovon jedoch folgends das Wesentliche resümiert wird. Die Beobachtungen sind unter den im 8. Kapitel im Allgemeinen angegebenen Maßregeln angestellt, und die Bezeichnungen hier wie dort zu verstehen. Zu der daselbst gegebenen allgemeinen Darstellung der Methode wird es jedoch nötig sein, folgends noch einige ergänzende Erörterungen zu fügen.
Die speziellen Maßregeln bei den folgenden Versuchen waren diese:
Bei meinen eigenen Versuchen wurden immer gestielte Schenkelzirkel mit eingelassenen Nähnadelspitzen (Länge der Schenkel 5 par. Duod.-Zoll) angewandt, und diese bei der Applikation an den Stielen gefaßt. Wo nicht (wie bei Reihe IV und teilweise VI) besonders bemerkt ist, daß die Applikation der Zirkel durch einen Gehilfen geschah, fand Selbstapplikation derselben statt. Die Reihe VI hat u. a. den Zweck, den verschiedenen Erfolg beider Applikationsweisen zu bestimmen. Bei den Beobachtungen am Vordergliede der Finger (Reihe II, V, VI) wurde von mir die eine Zirkelspitze stets in die Gelenkfuge zwischen dem vorderen und mittleren Fingergliede, und die andere nach vorn auf das Vorderglied aufgesetzt. Dies geschah, wie überhaupt die Versuche, ohne Zuziehung des Gesichtssinnes, indem man sich bald übt, die rechte Stelle auch ohne das zu treffen.
Stets wurden von mir je 10 Beobachtungen unter ganz denselben Umständen (mit derselben Normaldistanz, auf derselben Hautstelle, bei derselben Zeit- und Raumlage der Zirkel) unmittelbar hinter einander angestellt; ausgenommen in Reihe I bei den Beobachtungen an der Stirne, deren Haut zu empfindlich ist, um eine so oft hinter einander wiederholte Applikation der Zirkelspitzen auf derselben Stelle zu vertragen, und in Reihe II am Finger, wo die mitzugezogene kleine Distanz 5 d wegen der Nähe der Zirkelspitzen an einander die Entstehung eines Reizzustandes erleichterte.
Wenn mehrere Normaldistanzen in derselben Reihe geprüft wurden, wurden sie stets hinter einander durchlaufen, und an verschiedenen Tagen mit auf- und absteigender Folge derselben gewechselt, so wie auch in der Zeit- und Raumlage der Zirkelapplikation ein ganz regelmäßiger Wechsel nach Fraktionen à m = 10 oder nach Tagen beobachtet ward.
Wenn der Normalzirkel bei der Applikation mit der linken, der Fehlzirkel mit der rechten Hand gehalten wurde, ist dies mit L bezeichnet, umgekehrt mit R; — wenn der Normalzirkel zuerst, der Fehlzirkel zuzweit appliziert wurde, ist dies mit I, umgekehrt mit II bezeichnet 1); so daß hiernach 4 Zeit-Raumlagen
I L, II L, I R, II R
unterscheidbar sind, wovon jedoch in Reihe I bloß I L und I R in Anwendung kamen. Wenn beide Zirkel in dieselbe Hand gefaßt wurden, um an der anderen Hand Versuche damit anzustellen, kommt statt der Fassung R und L die Fassung mit dem oberen und unteren Teile der Hand in dem, Tb. II, Kap. 28 Anmerk. angegebenen Sinne in Betracht, welche durch 0 und U unterschieden wird.
Die Fraktionierung bei der Berechnung der von mir angestellten Reihen ist stets auf 10 Beobachtungen geschehen, welche, mit Ausnahme bei Reihe I und II, auch stets unmittelbar hinter einander angestellt waren, indem die mittlere Fehldistanz für je 10 Beobachtungen besonders bestimmt, die reinen Fehler als Differenzen der einzelnen Fehldistanzen von ihrer mittleren berechnet, und die solchergestalt fraktionsweise erhaltenen reinen Fehlersummen zur Gesamtsumme åD zusammengelegt wurden. Indem nun m die Zahl der Beobachtungen jeder Einzelfraktion, µ die Anzahl der Fraktionen bedeutet, aus denen jeder Wert åD in den folgenden Versuchstabellen abgleitet ist, ist µm die Zahl der Einzelbeobachtungen, die dazu beigetragen haben; für die Summenspalten in den Tabellen jedoch µm noch mit der Zahl der summierten Posten multipliziert zu denken. Den mittleren Fehler e erhält man dann durch Division von åD mit der Zahl der dazu beitragenden Fehler.
Das Vorige betraf wesentlich nur die eigenen Beobachtungsreihen (I, II, V, VI). Die Volkmann’schen (III, IV) sind mit anderen Zirkeln, deren Einrichtung ich nicht genau angeben kann, ohne Unterscheidung besonderer Zeit- und Raumlage, die nicht eben wesentlich dabei war, und mit anderer Zusammenfassung der Beobachtungen angestellt, auch andere Maßeinheiten dabei angewandt, worüber bei der speziellen Mitteilung der Reihen das Nötige.
Um die richtige Auslegung der Zahlen in den Tabellen jedenfalls zu sichern, erläutere ich die erste Zahl der ersten Versuchstabelle.
Unter D = 15 findet sich hier für I L die Zahl 32,7, indes über der Tabelle m = 10, µ = 5 steht, das heißt: bei einer Normaldistanz D = 15 halbe pariser Dezimallinien, in der Zeit-Raumlage IL wurde durch mµ = 50 Beobachtungen, also durch 50 reine Einzelfehler eine Fehlersumme åD= 32,7 halben pariser Dezimallinien erhalten, welche durch Berechnung aus 5 Fraktionen à m = 10 abgeleitet ist, was als e für 1 Fehler gibt 0,654 halbe pariser Dezimallinien. Eben so sind alle anderen Zahlen derselben Tabelle unter den Rubriken I L, I R auszulegen. Die Summenzahl 66,5 für I L und I R bei D = 15 wird dann, als für die doppelte Zahl Beobachtungen geltend, natürlich mit 100, statt 50 zu dividieren sein, um e für 1 Beobachtung zu geben, und noch mit 31/30, wenn man wegen des endlichen m korrigieren und damit e1 erhalten will. Der konstante Fehler c wird immer als durchschnittlicher für 1 Beobachtung angegeben. Die Zahl der Beobachtungen, aus denen man ihn ableitet, d. i. die Größe des m, hat nicht eben so wie bei åD einen Einfluß auf seine Größe, sondern nur auf die Sicherheit seiner Bestimmung.
Wo Beobachtungen bei 4-facher Zeit-Raumlage angestellt sind, werden die allgemein mit c bezeichneten konstanten Fehler speziell genannt
c1 c2
c3 c4
bei I
L II L I
R II R
oder I U II
U I O II O
Derselbe läßt sich dann, wie Th. II, Kap. 28 ausführlicher auseinandergesetzt ist, in eine von der Zeitlage abhängige Komponente p, eine von der Raumlage abhängige Komponente q, und eine von beiden unabhängige Komponente s, welche wahrscheinlich den, Th. II, Kap.28 angegebenen Ursprung hat, analysieren, indem man setzt
Wo, wie bei Reihe I, bloß Beobachtungen bei I L und I R vorliegen, stehen bloß die Gleichungen
c1 =
p
+ q + s
c3 = p
- q + s
zu Gebote, und man kann den konstanten Fehler dann bloß in eine von der Raumlage abhängige Komponente q und eine davon unabhängige p + s trennen, ohne p + s selbst trennen zu können.
In Th. I, S. 125. 127 habe ich
von mehreren Korrektionen gesprochen, welche an der reinen Fehlersumme
åD
oder dem daraus abgeleiteten Mittelfehler ![]() angebracht werden können, wovon die wichtigste die wegen des endlichen
m
ist (Th. II, Kap. 27), nach welcher åD
oder e noch mit
angebracht werden können, wovon die wichtigste die wegen des endlichen
m
ist (Th. II, Kap. 27), nach welcher åD
oder e noch mit ![]() zu multiplizieren ist. Da ich diese, bisher noch nicht hergeleitet gewesene,
wichtige Korrektion im Folgenden mehrfach anwende, will ich die Herleitung
derselben unter dem 1. Zusatz zu diesem Kapitel beifügen. Das Verständnis
dieser Herleitung setzt eine etwas nähere Bekanntschaft mit der mathematischen
Fehlertheorie voraus. Ohne Korrektion werde der aus den reinen Fehlern
abgeleitete Mittelfehler mit e, nach
der Korrektion wegen des endlichen m mit e1bezeichnet,
so daß
zu multiplizieren ist. Da ich diese, bisher noch nicht hergeleitet gewesene,
wichtige Korrektion im Folgenden mehrfach anwende, will ich die Herleitung
derselben unter dem 1. Zusatz zu diesem Kapitel beifügen. Das Verständnis
dieser Herleitung setzt eine etwas nähere Bekanntschaft mit der mathematischen
Fehlertheorie voraus. Ohne Korrektion werde der aus den reinen Fehlern
abgeleitete Mittelfehler mit e, nach
der Korrektion wegen des endlichen m mit e1bezeichnet,
so daß
![]() .
.
Außer dieser Korrektion habe ich Th. I, S. 127 noch zweier, unter Umständen anzubringender, Korrektionen von åD und e erwähnt, der Korrektion wegen der Größe der Intervalle und wegen Schätzung der Einteilung, die meist zu vernachlässigen sind, und von denen die zweite hier überhaupt nicht in Betracht kommt, da keine Schätzung von Zwischenteilen am Maßstabe stattfand; die erste aber nicht unzweckmäßig bei den Versuchen der Reihe VI zu berücksichtigen ist; da hier der Mittelfehler (bei Abteilung V) nicht viel größer als 0,1 d, d. i. als das kleinste Intervall des Maßstabes ist. Ich gebe hier diese Korrektion nachträglich kurz und für praktischen Zweck genügend an, und füge das Theoretische darüber unter dem 2. Zusatze bei.
Sei die wegen der Größe
der Intervalle noch nicht korrigierte, mithin falsche, Fehlersumme åDund
der unkorrigierte Mittelfehler ![]() ;
seien die kleinsten unterschiedenen Intervalle der Einteilung von der Größe
i,
so findet sich die korrigierte oder wahre Fehlersumme SD
aus
der falschen åD durch folgende Gleichung
;
seien die kleinsten unterschiedenen Intervalle der Einteilung von der Größe
i,
so findet sich die korrigierte oder wahre Fehlersumme SD
aus
der falschen åD durch folgende Gleichung
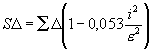
so wie der korrigierte Mittelfehler e1aus dem falschen durch
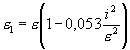
Ist also z. B. i = e , so hat man
SD = 0,947 åD
was eine nicht zu vernachlässigende Korrektion ist.
Wäre i nur = 1/4e
, so wäre ![]() =
1/16
mithin
SD
=
0,9967
åD .
=
1/16
mithin
SD
=
0,9967
åD .
Hiernach kann man selbst bemessen, inwiefern die Natur der Beobachtungen und Aufgaben es nötig erscheinen läßt, sich auf diese übrigens sehr einfache Korrektion einzulassen. Ich bin bloß bei der Reihe VI darauf eingegangen.
Bei den sehr kleinen konstanten Fehlem, die zum Teil im Folgenden vorkommen, kann man mehrfach fragen, ob ihr Dasein nicht bloß auf unausgeglichenen Zufälligkeiten ruht. Um dies zu beurteilen, muß man den wahrscheinlichen Fehler des konstanten Fehlers suchen, und sehen, ob er in erheblichem Verhältnisse durch die Größe des konstanten Fehlers selbst überschritten wird, was sehr einfach nach folgender Regel mittelst des zu dem Werte c gehörigen Wertes åD geschehen kann.
Sei M = mµ die Gesamtzahl der Beobachtungen, aus denen c und mithin das zugehörige åD abgeleitet ist, wo m wie gewöhnlich die Fehlerzahl einer Fraktion, µ die Zahl der Fraktionen ist, die zu åD beigetragen haben, so ist der wahrscheinliche Fehler w von c
![]() .
.
So gehört in der ersten Beobachtungsreihe (bei D = 15, I L) zur Fehlersumme åD = 32,5 der konstante Fehler + 0,89. Da åD und c aus 50 Beobachtungen abgeleitet sind, so ist M= 50, und da bei der Ableitung Fraktionen à 10 angewendet sind, so ist m = 10; hiernach
![]()
Der konstante Fehler c also, wenn wir, wie gewöhnlich, den wahrscheinlichen Fehler mit ± beifügen, so zu schreiben
Die vorige allgemeine Regel zur Bestimmung w begründet sich wie folgt: der wahrscheinliche Fehler des konstanten Fehlers c kommt mit dem wahrscheinlichen Fehler der mittleren Fehldistanz (= Normaldistanz + c) überein, da der wahrscheinliche Fehler einer Größe sich nicht ändert, wenn man zu dieser eine feste Größe (Normaldistanz) zugefügt oder davon abgezogen denkt. Den wahrscheinlichen Fehler der mittleren Fehldistanz aber kann man aus den Abweichungen, welche die einzelnen Fehldistanzen von derselben haben, d. i. den reinen Fehler D bestimmen; was entweder in der gewöhnlichen Weise aus der Summe der Fehlerquadrate und dem daraus abgeleiteten quadratischen mittleren Fehler eq nach der Formel
![]() ,
,
aber auch merklich gleichgeltend mittelst der einfachen Fehlersumme und des daraus abgeleiteten einfachen mittleren Fehlers e1nach der Formel
![]()
geschehen kann, insofern eq und e1 durch das (theoretisch begründete und von mir experimental verifizierte) normale Verhältnis
![]()
verknüpft sind. e1 aber wird erhalten, indem man åD mit der Gesamtzahl der Beobachtungen M dividiert und wegen des endlichen m korrigiert, wodurch man zu der angegebenen Formel gelangt.
Die Erörterung, wie die obigen speziellen Wahrscheinlichkeitsregeln bezüglich des Verhältnisses von c zu w gefunden sind, würde hier zu weit führen; auch beruht diese Bestimmung auf hinreichend bekannten Prinzipien.
Hat man die wahrscheinlichen Fehler w für c1, c2, c3, c4 insbesondere bestimmt, und die zugehörigen Werte von w = w1, w2 ,w3, w4 gefunden, so erhält man daraus leicht auch den wahrscheinlichen Fehler der Komponenten p, q, s, welcher W heiße. Derselbe ist nämlich, wenn diese Komponenten nach den Gleichungen (s. o.) aus allen 4 Werten c solidarisch bestimmt sind, für alle drei gleichgeltend
![]() .
.
Hat man irgendwelche der Komponenten des konstanten Fehlers bloß aus zwei Werten von c, z. B. c1, c2 oder c1, c3 bestimmt, so ist auch der Wert des wahrscheinlichen Fehlers dieser Komponente nur
![]() oder
oder![]() u. s. f.
u. s. f.
Auch jede Komponente des konstanten Fehlers wird man nach gleichem Prinzipe als den ganzen konstanten Fehler als Sache bloß unausgeglichener Zufälligkeiten ansehen können, wenn ihre Größe nicht die des wahrscheinlichen Fehlers W erheblich übersteigt.
Hat man die Werte des konstanten Fehlers c für die µ Fraktionen einer größeren Beobachtungsreihe besonders bestimmt, wozu ich in Reihe VI Beispiele gebe, so kann man auch die Abweichungen, welche die µ Fraktionswerte des konstanten Fehlers vom mittleren c darbieten, und welche J heißen mögen, in Betracht ziehen, und diese Abweichungen benutzen, nach der gewöhnlichen Regel mittelst der Summe der Quadrate å (J ²) oder mittelst der einfachen Summe åJ einen wahrscheinlichen Fehler von c zu berechnen, ersteres mittelst der Formel
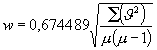
letzteres mittelst der Formel
![]()
wo µ die Zahl der Fraktionen und mithin Einzelwerte von c ist. Inzwischen hat der so berechnete wahrscheinliche Fehler nicht ganz gleiche Bedeutung mit dem, nach (s. o.) aus åD bestimmten, indem er wesentlichst mit abhängig ist von den, bei längeren Versuchsreihen nie leicht fehlenden, Variationen des konstanten Fehlers. Während jener bloß maßgebend ist für die von größeren und geringeren unregelmäßigen zufälligen Einflüssen abhängige Sicherheit der Bestimmung des konstanten Fehlers, ist dieser zugleich maßgebend für den Grad des Schwankens des konstanten Fehlers, und es können daher zwar beide Bestimmungsweisen (aus åD und åJ ) unter Umständen, wo das Schwanken gering ist, nahe übereinstimmende, unter Umständen aber auch ausnehmend abweichende Resultate geben, wie die Beispiele in Reihe VI beweisen. Um zu entscheiden, ob ein Schwanken statt gefunden habe, ist es daher nützlich, beide Bestimmungsweisen zu vergleichen.
Wo nichts besonders bemerkt ist, ist w im Folgenden immer aus åD nach der (s. o.) gegebenen Formel berechnet.
Unstreitig ist eine absolut reine Trennung der Fehler D von Variationen des konstanten Fehlers in Wirklichkeit durch keine Fraktionierung und fraktionsweise Behandlung der Beobachtungsreihen möglich, und leidet selbst an begrifflichen Schwierigkeiten. Wenn man aber alle zu vergleichenden Beobachtungen stets in Fraktionen von derselben mäßigen Zahl unter vergleichbaren Umständen anstellt, und bei der Berechnung stets zu gleichem m zusammenfaßt, so wird die daraus hervorgehende Unterscheidung der Variationen des konstanten Fehlers und der reinen Fehler D immer nützlich, und diese fraktionsweise Behandlung der unfraktionierten Behandlung, wo sich die Variationen des konstanten Fehlers mit dem Fehler D ununterscheidbar mischen, vorzuziehen bleiben.
Es wird nicht ohne Nutzen sein, wenn ich hier auch noch den wahrscheinlichen Fehler der reinen Fehlersumme åD und des daraus abgeleiteten Mittelfehlers e angebe. Man erhält ihn, indem man respektiv åD oder e mit
![]()
multipliziert 2). Nehmen
wir wie gewöhnlich
m = 10 , so ist l
= 0,16115; wonach man nach einer mittleren Wahrscheinlichkeit jede reine
Fehlersumme so wie jeden reinen Mittelfehler aus einer Fraktion à
m
= 10 ungefähr um 1/6 ihrer
Größe falsch bestimmt. Nicht, daß dies bei jeder einzelnen
Fraktion wirklich stattfände; aber wenn man viele Fraktionen mit m
= 10 vor sich hat, ist der Irrtum eben so oft über als unter dem angegebenen.
Um den wahrscheinlichen Fehler einer totalen Fehlersumme aus µ
Fraktionsummen von gleichen m zu bestimmen, hat man die µ
Fraktionsummen einzeln zum Quadrat zu erheben, aus der Summe dieser Quadrate
die Wurzel zu ziehen, und diese mit l , d. i. ![]() ;
also im Falle von m = 10 mit 0,16115 zu multiplizieren.
;
also im Falle von m = 10 mit 0,16115 zu multiplizieren.
2) Astronom. Jahrb. f. 1834. S. 293.
Es würden sich noch viele nützliche Bestimmungen über die Wahrscheinlichkeitsverhältnisse der Fehler hinzufügen lassen, aber dies würde hier zu weit führen.
I. Fechner. Okt. 1857 – Juli 1858.)
Stirn: Neun quere Distanzen. Einheit 1 d. Gesamtzahl der Beobachtungen 900, verteilt auf 100 Tage à 9 Beobachtungen.
Die Distanzen werden folgends in doppelter
Bestimmung gegeben, als D, wie sie der Spannweite des auf die Haut
aufgesetzten Zirkels direkt entsprechen, als D', wie sie der wirklichen
Länge der in dieser Hautstrecke begriffenen Hautstrecke entsprechen.
Da nämlich die Stirn etwas gekrümmt ist, so fällt beides
nicht zusammen. Um die zu einander gehörigen Werte von D und
D'
zu bestimmen, wurde ein Papierstreifen über die Stirn gelegt, und
durch den Zirkel bei der Spannweite D Punkte in derselben markiert,
deren Abstand dann gemessen wurde, nachdem der Streifen eben ausgebreitet
worden. Aus mehreren solchen Bestimmungen wurde das Mittel genommen. Die
Werte waren:
| D = | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 60 |
| D' = | 15 | 20 | 25,3 | 30,5 | 36 | 41,5 | 46,9 | 52,9 | 65,7 |
Die bei der letzten Distanz D = 60 oder D' = 65,7 erhaltenen Werte der folgenden Tabellen können füglich außer Acht bleiben, indem die große Abweichung derselben von den übrigen sehr wohl darauf geschoben werden kann, daß die Zirkelspitzen wegen der hier sehr erheblich werdenden Krümmung der Stirn sehr schief auf die Haut auftreffen, so daß die Beobachtungen hier mit den anderen so gut wie unvergleichbar werden. Daher sind die bei dieser Distanz erhaltenen Werte in der Tabelle eingeklammert und bei der Ziehung der Totalsumme nicht mit zugezogen, welche also nur die Werte bei den Distanzen bis D = 50 inklusiv befaßt. Es konnte jeden Tag die Reihe der 9 Distanzen aus dem (s. o.) angegebenen Grunde nur einmal durchlaufen werden.
åD ( m = 10, µ = 5) 3).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
102,8 |
|
|
|
|
(150,8) |
c.
| D | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | (60) |
| I L | +0,90 | +1,20 | +0,92 | +0,85 | +1,12 | +1,14 | +0,61 | +0,43 | (+0.49) |
| I R | +0,11 | +0,36 | +0,24 | +0,42 | +0,27 | - 0,10 | +0,10 | +0,20 | (+0,17) |
3) Im Folgenden ist die berichtigte Tabelle aus: In Sachen S. 217 f. mitgeteilt.
Man sieht von D = 15 bis D = 25 ein deutliches Ansteigen der Fehlersumme åD mit D, welches sogar für I L allein genommen bis D = 30 sehr genau proportional mit D vorschreitet, aber darüber hinaus kein deutliches Wachstum mehr, sondern nur Unregelmäßigkeiten, die sich bei weiterer Fortsetzung der Beobachtungen zum Teil noch ausgeglichen haben könnten. Bestimmt man den Mittelfehler als durchschnittlichen für die Beobachtungen bei den 6 Distanzen D = 25 bis D = 50, innerhalb deren merkliche Konstanz (für I L und I R zusammengenommen) besteht, so findet man
4) Vgl. In Sachen S. 218.
Der konstante Fehler ist mit einer einzigen Ausnahme bei allen Distanzen in beiden Lagen positiv; aber, wie man sieht, bei der Lage I R (Fassung des Normalzirkels in der Rechten) überall kleiner als bei der Lage I L (Fassung in der Linken), was ein Beispiel für den nicht zu vernachlässigenden Einfluß der Fassungsweise der Zirkel ist; hingegen ist keine gesetzliche Abhängigkeit der konstanten Fehler von der Größe der Distanz bemerklich. Für die Komponenten q und p + s des konstanten Fehlers erhält man im Mittel für alle Distanzen unter Ausschluß von D = 60
q = +0,372; p + s = +0,527 5).
Schon früher (1856 und 1857) habe ich ähnliche Versuchsreihen an der Stirn mit ähnlichen Resultaten angestellt, die ich übergehe, weil sie mit ungestielten Zirkeln und minder sorgfältiger Verhütung der Reizung der Stirnhaut angestellt waren.
5)Vgl. In Sachen S. 218.
m = 10, m = 5.
|
|
|
|||
| D | 5d | 10d | 5d | 10d |
| I U | 7,28 | 6,14 | 0,000 | - 0,240 |
| II U | 8,52 | 9,02 | - 0,230 | - 0,296 |
| I O | 7,18 | 8,50 | + 0,054 | - 0,272 |
| II O | 8,18 | 8,30 | - 0,292 | - 0,444 |
| Summe | 31,16 | 31,96 | — | — |
Hier zeigt sich die Fehlersumme åD fast unverändert bei verdoppelter Distanz, e1 im Mittel aus allen Beobachtungen 0,163d.
Die Berechnung der Komponenten des
konstanten Fehlers gibt folgendes Resultat:
|
|
|
|
| p | + 0,146 | + 0,057 |
| q | + 0,002 | - 0,045 |
| s | - 0,117 | - 0,313 |
| s1 | - 0,146 | - 0,342 |
| s2 | - 0,088 | - 0,284 |
| W | 0,00963 | 0,00994 |
Man sieht hier die Komponente s von bemerkenswerter Größe und bei D = 10d in den Doppelwerten so nahe stimmend, als man es bei der verhältnismäßig geringen Zahl Beobachtungen erwarten kann, wogegen bei D = 5d keine sonderliche Übereinstimmung von s1 und s2 in den absoluten Werten besteht, indes die immer noch beträchtliche Größe und Übereinstimmung des Vorzeichens von s1 und s2, so wie geringe Größe des nach der Regel berechneten wahrscheinlichen Fehlers 0,00994 beweist, daß doch auch hier der Fehler s wirklich besteht. Nur der Fehler q bei D = 5 kann überhaupt hiernach durch Zufälligkeiten erklärt werden.
III. Volkmann (April 1857).
Mittelfinger. Vorderglied, Volarseite, vier Längsdistanzen. Einheit 1 Millimeter. Ohne Rücksicht auf besondere Zeit- und Raumlage. 264 Beobachtungen.
m = 33, µ = 2.
|
|
|
|
|
|
| åD | 6,68 | 9,13 | 12,70 | 12,13 |
| c | + 0,045 | + 0,131 | + 0,012 | - 0,018 |
| e1 | 0,102 | 0,140 | 0,194 | 0,216 |
Das Wachstum von åD oder e1 mit den Distanzen war also viel bedeutender als bei mir in Reihe II, aber doch auch bei Weitem nicht proportional mit D.
IV. Volkmann (Januar und Februar 1858).
Linker Handrücken, vier quere Distanzen. Einheit 1 pariser Linie. Applikation der Zirkel durch einen Gehilfen ohne Rücksicht auf besondere Zeit- und Raumlage. 480 Beobachtungen.
m = 20, µ = 6.
|
|
|
|
|
|
| åD | 67,2 | 60,8 | 86,8 | 83,1 |
| c | + 0,45 | + 0,47 | + 0,37 | + 0,31 |
| e1 | 0,569 | 0,515 | 0,735 | 0,704 |
V. Fechner (Nov. 1857 bis April 1858).
Fünf Finger der linken Hand. Vorderglied, Volarseite, auf jedem Finger 1 Längsdistanz = 10d. Im Ganzen 6400 Beobachtungen, verteilt auf 64 Beobachtungstage à 100 Beobachtungen.
An jedem Tage alle 5 Finger in zwei Zeit-Raumlagen mit 20 Beobachtungen (10 für eine Lage) durchlaufen.
Es bedeutet folgends D Daumen, Z Zeigefinger, M Mittelfinger, G Goldfinger, K kleiner Finger.
Diese Reihe ist im Zusammenhange
mit einer Reihe nach der Methode der Äquivalente an denselben 5 Fingern
angestellt, so daß die Methode der mittleren Fehler und die der Äquivalente
nach je zwei Tagen wechselten. Hier sind bloß die Resultate nach
der Methode der mittleren Fehler angeführt; da es für jetzt zu
weit führen würde, auch die der anderen Methode zu berücksichtigen.
m = 10, µ = 32.
|
|
|
|
|
|
|
|
|
|
I U | 77,92 | 67,54 | 67,36 | 78,80 | 74,94 |
| II U | 80,70 | 65,34 | 73,54 | 69,14 | 75,00 | |
| I O | 68,56 | 54,68 | 68,03 | 68,40 | 71,40 | |
| II O | 76,00 | 64,54 | 63,34 | 70,26 | 71,92 | |
|
|
303,18 | 252,10 | 272,27 | 286,60 | 293,26 | |
|
|
I U | - 0,0557 | - 0,0882 | - 0,0075 | + 0,0625 | - 0,0438 |
| II U | - 0,1700 | - 0,0953 | - 0,2066 | - 0,2766 | - 0,2582 | |
| I O | - 0,2691 | - 0,3950 | - 0,2222 | - 0,1641 | - 0,2432 | |
| II O | - 0,3700 | - 0,3310 | - 0,3779 | - 0,3816 | - 0,4303 | |
|
|
0,2448 | 0,2035 | 0,2198 | 0,2313 | 0,2367 | |
| p | + 0,0538 | - 0,0142 | + 0,0887 | + 0,1392 | + 0,1002 | |
| q | + 0,1034 | + 0,1356 | + 0,0965 | + 0,0829 | + 0,0929 | |
| s | - 0,2162 | - 0,2274 | - 0,2036 | - 0,1899 | - 0,2439 | |
| s1 | - 0,2128 | - 0,2096 | - 0,1927 | - 0,2204 | - 0,2508 | |
| s2 | - 0,2196 | - 0,2452 | - 0,2144 | - 0,1596 | - 0,2370 | |
|
|
0,00579 | 0,00514 | 0,00520 | 0,00548 | 0,00560 | |
Hiernach findet die größte Fehlersumme 303,18 beim Daumen, die kleinste 252,10 beim Zeigefinger statt, der also die größte Unterschiedsempfindlichkeit unter den 5 Fingern zeigt.
Der wegen des endlichen m korrigierte Mittelfehler e1 ist im Mittel aller 5 Finger bei allen Lagen = 0,2272d = 1/44D. Der konstante Fehler c ist mit einer einzigen Ausnahme bei allen Fingern in allen Lagen negativ, was von der großen negativen Komponente s abhängt, wogegen p, q sich positiv finden, mit Ausnahme von p bei Z, eine Ausnahme, die um so auffälliger ist, als sie in Reihe II und VI unter ähnlichen Versuchsumstanden am Zeigefinger nicht stattfindet. Bei Z und G stimmen die Doppelwerte von s nicht zum besten, bei den drei anderen Fingern aber sehr gut. Der wahrscheinliche Fehler W von p, q, s ist überall zu klein, um dieselben als auf Zufall beruhend anzusehen.
Im Mittel für alle fünf Finger hat man
Wenn ich den Normalzirkel mit der Spannweite 10d zuerst, den Fehlzirkel zuzweit applizierte, fiel vermöge dieses Einflusses der Zeitlage die Fehldistanz um + 0,0735d zu groß aus, oder ward statt der Normaldistanz 10 die Fehldistanz 10,0735 gefunden. Wenn der Normalzirkel zuzweit appliziert wurde, so fiel die Fehldistanz um eben so viel zu niedrig aus, oder ward statt 10 erhalten 9,9265, was mit dem vorigen Resultate solidarisch ist.
Wenn der Normalzirkel mit dem unteren Teile, der Fehlzirkel mit dem oberen Teile der Hand (vgl. Kap. 28) gefaßt wurde, so fiel die Fehldistanz um 0,1023 zu groß, im umgekehrten Falle zu niedrig aus.
Abgesehen von diesem Einflusse der Zeit- und Raumlage fiel die Fehldistanz aus dem Kap. 27 angegebenen Grunde um 0,2160 zu niedrig aus.
Diese drei Einflüsse kombinieren sich additiv oder subtraktiv, je nachdem sie in demselben Sinne oder in entgegengesetztem Sinne sind. Alle drei sind in demselben Sinne bei IIO, daher die dazu gehörigen Werte c durchschnittlich die größten, wogegen bei I U der große Fehler s durch die gemeinsame Entgegensetzung von p und q am meisten kompensiert wird, daher hier die kleinsten Werte c.
Der obigen Berechnung der reinen Fehlersummen liegt die von mir gewöhnlich angewandte Fraktionierung auf m = 10 unter. Um aber den Einfluß zu zeigen, den nach Th. I, S. 124 die mehr oder weniger weit getriebene Fraktionierung auf die Größe der reinen Fehlersumme hat, ist die vorige Beobachtungsreihe außerdem auch unter Anwendung von m = 160, und endlich ganz unfraktioniert für jeden Finger und jede Lage, d. i. aus m = 320, berechnet worden. Das für alle 4 Lagen zusammengezogene Resultat stellt sich mit dem vorhin erhaltenen wie folgt zusammen.
åD .
| D | Z | M | G | K | Summe | |
| m = 10, µ = 128 | 303,18 | 252,10 | 272,27 | 286,60 | 293,26 | 1407,41 |
| m = 160, µ = 8 | 350,64 | 285,91 | 315,51 | 337,34 | 336,88 | 1626,29 |
| m = 320, µ= 4 | 354,76 | 291,19 | 320,24 | 345,34 | 349,25 | 1660,78 |
Man sieht hier ausnahmslos die Größe von åD mit der Größe des angewandten m wachsen.
Die von mir angewendete Korrektion
wegen des endlichen
m durch Multiplikation der Werte mit ![]() hebt bloß den schwächeren Teil dieses Wachstums, indem dasselbe
nachweislich hauptsächlich auf der Variation der konstanten Fehler
im Laufe der langen Versuchsreihe beruht, welche beim Zusammenschlagen
vieler zu verschiedenen Zeiten gewonnener Beobachtungen in eine Fraktion
die daraus abgeleitete Fehlersumme vergrößert, daher der Vorzug,
den ich kleineren Fraktionen aus Beobachtungen, die im Zusammenhange gewonnen
sind, gebe, indem die Korrektion wegen des endlichen m nach Maßgabe
zulänglicher werden muß, als dieser der reinen Fehlersumme an
sich fremdartige Zuwachs wegfällt. Das wirklich eine Variation des
konstanten Fehlers im Laufe der Beobachtungsreihe stattgefunden, ergibt
sich aus der unten folgenden Anführung für die zwei nach der
Zeit unterschiedenen Haupt-fraktionen der Beobachtungsreihe.
hebt bloß den schwächeren Teil dieses Wachstums, indem dasselbe
nachweislich hauptsächlich auf der Variation der konstanten Fehler
im Laufe der langen Versuchsreihe beruht, welche beim Zusammenschlagen
vieler zu verschiedenen Zeiten gewonnener Beobachtungen in eine Fraktion
die daraus abgeleitete Fehlersumme vergrößert, daher der Vorzug,
den ich kleineren Fraktionen aus Beobachtungen, die im Zusammenhange gewonnen
sind, gebe, indem die Korrektion wegen des endlichen m nach Maßgabe
zulänglicher werden muß, als dieser der reinen Fehlersumme an
sich fremdartige Zuwachs wegfällt. Das wirklich eine Variation des
konstanten Fehlers im Laufe der Beobachtungsreihe stattgefunden, ergibt
sich aus der unten folgenden Anführung für die zwei nach der
Zeit unterschiedenen Haupt-fraktionen der Beobachtungsreihe.
In Th. l, S. 213 habe ich gelegentlich
bemerkt, daß, wenn man die mit der doppelten Fehlerzahl multiplizierte
Summe der Fehlerquadrate
å (D
²) mit dem Quadrate der Fehlersumme (åD
)2dividiert, approximativ die Ludolf’sche
Zahl p erhalten wird, welche approximative Zahl
P
heiße, so daß man hat
![]()
wenn m die in die Summe eingehende Fehlerzahl (bei µ = 1) ist. Unsere Reihe kann als Beispiel dienen. Ich gebe für Daumen unter Anwendung von m = 160, µ = 1 (indem ich die 320 betragende Gesamtzahl der Beobachtungen für jede Lage in zwei Fraktionen nach der Zeit teilte, und für jede besonders åD und å (D ²) bestimmte) den Wert von åD und å (D ²) mit dem daraus nach obiger Formel berechneten P in folgender Tabelle.
m = 160, µ = 1.
|
|
|
|
|
| I U. 1. Frakt. | 43,97 | 18,75 | 3,103 |
| 2. - | 42,16 | 16,52 | 2,974 |
| II U. 1. - | 42,91 | 17,56 | 3,052 |
| 2. - | 46,23 | 21,87 | 3,275 |
| I O. 1. - | 49,24 | 25,48 | 3,363 |
| 2. - | 40,86 | 17,62 | 3,377 |
| II O. 1. - | 48,28 | 21,14 | 2,902 |
| 2. - | 36,99 | 15,11 | 3,534 |
| Summe | 350,64 | 154,05 | 25,580 |
Das Mittel der 8 P-Werthe ist 3,198. Die entsprechend berechneten Mittelwerte für alle 5 Finger waren:
D Z M G K
3,198; 3,183; 3,072; 3,144; 3,145
Das Totalmittel aus diesen 5 Mittelwerten, wozu also im Ganzen 40 Werte P, jeder aus 160 Beobachtungen bestimmt, beigetragen haben, ist
3,148
was vom Normalwerte p = 3,142 bis auf die letzte, durch Abrundungen unsichere, Dezimale völlig übereinkommt.
Hieraus läßt sich leicht das konstante Verhältnis
![]()
ableiten, wovon Th. I, S. 123 die Rede war.
Des Weiteren bemerke ich gelegentlich,
daß man approximativ die Grundzahl der natürli-chen Logarithmen
e
erhält, wenn man die Totalsumme der Fehler åD
mit der Summe der Fehler, welche den quadratischen Mittelfehler ![]() an Größe übersteigen, dividiert, und den Quotienten zum
Quadrate erhebt. Das, hiernach entsprechend wie oben das Totalmit-tel von
P
aus 40 Partialwerten (am = 160) berechnete, Totalmittel fand sich
2,707 statt des Normalwertes
e = 2,718.
an Größe übersteigen, dividiert, und den Quotienten zum
Quadrate erhebt. Das, hiernach entsprechend wie oben das Totalmit-tel von
P
aus 40 Partialwerten (am = 160) berechnete, Totalmittel fand sich
2,707 statt des Normalwertes
e = 2,718.
Obwohl ich nicht finde, daß diese merkwürdigen Verhältnisse schon ausdrücklich bemerkt worden wären, lassen sie sich doch mit manchen anderen interessanten Verhältnissen leicht aus der mathematischen Fehlertheorie mittelst des für die Wahrscheinlichkeit der Fehler geltenden bekannten Ausdruckes, in welchen p und e eingehen, ableiten, was für den, in dieser Theorie Bewanderten keiner besonderen Ausführung bedürfen wird, übrigens anderwärts von mir mit weiteren Versuchsbelegen dargelegt werden soll. Die angegebenen Verhältnisse p , e gelten streng für eine unendliche Zahl unter vergleichbaren Umständen gewonnener Fehler und schwanken bei wiederholter Bestimmung aus einer endlichen Zahl, wie man sich aus obigem Beispiele mit 8 Bestimmungen von P überzeugen kann, um das Normalverhältnis, eine Schwankung, die in um so weiteren Grenzen statt hat, je kleiner m ist. Nur bei sehr kleinem Werte m stellt sich im Mittel vieler Bestimmungen eine merkliche Abweichung vom Normalwerte heraus, welche mit der Kleinheit von m wächst, und bei etwas großem m verschwindend klein ist. Diese Abweichung läßt sich nach der Korrektion der Fehlerquadratsumme und des Quadrates der Fehlersumme wegen des endlichen m durch einen allgemeinen Ausdruck bestimmen; wonach ein aus einer endlichen Zahl m abgeleitetes P normalerweise
![]() statt = p
statt = p
ist, was z. B. für m = 10 gibt P= 3,0166. 6)
6)
Berichtigungen hierzu In Sachen S. 218. Vgl. auch Poggendorffs. Ann. Jubelband.
S. 66 ff.
Im Laufe der langen mehrmonatlichen
Beobachtungsreihe nahm sowohl der variable als konstante Fehler allmälig
ab. Teilt man die ganze Reihe in zwei Hauptfraktionen nach der Zeit (jede
zu 32 Beobachtungstagen), so erhält man in Summa für alle 4 Lagen:
åD (m = 160, µ = 4).
| D | Z | M | G | K | Summe | |
| 1. Frakt. | 154,94 | 134,56 | 150,12 | 159,26 | 161,28 | 760,16 |
| 2. - | 148,24 | 117,54 | 122,15 | 127,34 | 131,98 | 647,25 |
| Verhältnis | 1,015 | 1,119 | 1,229 | 1,253 | 1,194 | 1,175 |
Im Ganzen also hatte sich die reine Fehlersumme von der 1. zur 2. Fraktion von 760,16 auf 647,25 vermindert; welche Zahlen das Verhältnis 1,175 haben.
Ferner fanden sich die Komponenten
des konstanten Fehlers im Mittel für alle 5 Finger wie folgt:
| 1. Frakt. | 2. Frakt. | |
| p | + 0,1006 | + 0,0465 |
| q | + 0,1260 | + 0,0785 |
| s | + 0,2281 | + 0,1942 |
Der Zeitfehler p und Raumfehler q hatten sich also von der ersten zur zweiten Fraktion sehr beträchtlich, der Fehler s doch merklich vermindert. Eine solche Änderung hatte nun aber nicht bloß von der ersten zur zweiten Hauptfraktion, sondern innerhalb jeder Hauptfraktion stattgefunden, und bei Zusammenfassung der Beobachtungen derselben zu m = 160 den variabeln Fehler vergrößert.
Bei den ungefähr 1 Stunde dauernden Beobachtungen jedes Tages wurden abwechselnd mit den Tagen die Finger in der Ordnung D. Z. M. G. K. und in der umgekehrten Ordnung durchlaufen , wovon Ersteres mit ® , Letzteres mit ¬ bezeichnet werde. Bei ® war die Aufmerksamkeit am frischesten beim Daumen, am meisten ermüdet beim kleinen Finger; bei ¬ war es umgekehrt. Es schien mir von Interesse, den hieraus hervorgehenden Einfluß zu untersuchen, welcher, wie man aus Folgendem sieht, nicht groß, doch sichtbar ist. Ich erhielt nämlich in Summa für alle 4 Lagen:
åD(m = 10, µ = 64)
| D | Z | M | G | K | |
| ® | 148,56 | 128,20 | 136,22 | 152,24 | 151,32 |
| ¬ | 154,62 | 123,90 | 136,05 | 134,36 | 141,94 |
Mit der wachsenden Übung verkürzte sich allmälig, bis zu einer gewissen Grenze, die Beobachtungszeit, welche für die 100 Versuche jedes Tages erforderlich war; indem man allmälig dahin kommt, die Entscheidung bei jedem Versuche schneller zu fällen, als anfangs. Das diese größere Schnelligkeit doch keine größere Ungenauigkeit in der Schätzung mitführte, beweist sich daraus, das vielmehr umgekehrt, im Fortschritte der Beobachtungsreihe, die Fehlersummen sieh verkleinerten. Aber auch, wenn ich aus derselben Versuchsperiode die Fehlersummen der Tage mit der größten und kleinsten Versuchsdauer vergleiche, finde ich keinen in Betracht kommenden Unterschied zwischen beiden. Manchen Tag kann man gar nicht fertig mit wiederholten Applikationen der Zirkel werden, ehe man sich entscheidet, anderemale ist man durchschnittlich viel schneller mit dem Urteile fertig; aber die langsamsten Entscheidungen sind nicht immer die besten. Hier folgen noch einige Daten über diese Verhältnisse.
Ich habe die Versuchsdauer nicht vom Anfange der Beobachtungsreihe herein, welche vom 21. Nov. 1857 bis 6. April 1858 dauerte, und auch später nicht an allen Tagen, aber an 32 verschiedenen Tagen vom 3. Jan. an bestimmt; und im Mittel 63,6 Min. gefunden. Wenn ich aber die Beobachtungsreihe vom 3. Jan. bis zum Schlusse in 4 gleiche Abteilungen von 24 Tagen teile, so wurden folgende mittlere Beobachtungszeiten darin gefunden:
2. - 67,3 - - - 8 - )
3. - 60,4 - - - 10 - )
4. - 60,5 - - - 10 - )
Die Beobachtungszeit schwankte überhaupt von 53 bis 76 Minuten. Ich stellte nun unter Ausschluß der früheren Periode, wo alle Beobachtungszeiten verhältnismäßig groß sind 7), aus der letzten Zeit vom 17. Febr. bis 6. April, wo größere und kleinere Zeiten unregelmäßig wechseln, die Fehlersummen für die Tage mit den 5 kleinsten Versuchsdauern (53, 84, 55, 56, 58 Min.) und mit den 5 größten Versuchsdauern (64, 64, 65, 66, 68 Min.) zusammen; und erhielt aus ersteren in Summa für alle Finger und alle Lagen (mit m = 10, µ = 50) åD = 1009,4, aus letzteren 995,6, was nur ganz unerheblich abweicht.
Linker Zeigefinger. Vorderglied, Volarseite, 1 Längsdistanz = 10d. Im Ganzen 1200 Versuche in 40 Versuchstagen, à 30 Beobachtungen.
Diese Versuche teilen sieh in drei, je 400 Beobachtungen enthaltende, Hauptabteilungen nach der Applikationsweise der Zirkel.
a) Applikation der Zirkel auf meinen Finger durch einen Gehilfen. Beobachter und Gehilfe sitzen sich gegenüber, der Gehilfe stützt den Arm, welcher den Zirkel appliziert, festeren Haltes wegen, auf den Tisch.
b) Selbstapplikation der Zirkel mit der rechten Hand auf den linken Zeigefinger.
g) Die Zirkel in vertikaler Lage neben einander in eine Schraubenzwinge eingespannt, und der Finger von einem zum anderen bewegt. Beide Zirkeldistanzen sind nahe an einander, einander parallel, senkrecht gegen die Vorderfläche des Körpers A B wie folgt angebracht:
b. .d
a. . c
A————————————————————B
wo a, b die Spitzen des einen, c, d die des anderen Zirkels bedeuten, und zwar wurde (nach Tagen wechselnd) die Normaldistanz einmal rechts (R), das anderemal links (L) genommen, worauf sich hier die Raumlage bezieht, indes bei a) und b) die Raumlage (O und U) auf obere und untere Fassung des Zirkels geht. Jeden Tag 3 Versuchssätze à 10 Beobachtungen hinter einander respektiv für a, b , g angestellt, a aus äußeren Gründen stets zuerst, indes b,g mit der zweiten und dritten Stelle wechselten.
Die Lagen sind mit eingeklammerten Ziffern wie folgt bezeichnet :
bei g .... IL
II
L IR
II R
m = 10, µ = 10.
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
170,49 | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b 0,1312 0,1311
g 0,1185 0,1178
Man sieht, daß die Applikationsweise
der Zirkel
a , d. i. durch einen Gehilfen, bei
Weitem die größte Fehlersumme åD
und demgemäß die größten Werte e1geliefert
hat; was davon abhängt, daß eine fremde Hand die Zirkel nicht
so gleichförmig zu applizieren vermag, als man es selbst kann, und
was beweist, wie viel zur Vergleichhaltung der Werte auf Vergleichbarkeit
der Manipulation bei den Versuchen ankommt.
b
und g weichen nicht sehr von einander ab, doch
ist g noch etwas vorteilhafter als b.
Der
mittlere Fehler
e1
beträgt bei g nur 0,1178 d, d. i. ![]() D.
D.
Während der variable Fehler bei a ) am größten ist, sind die konstanten Fehler c bei a ) am kleinsten, und q, s so klein, daß namentlich s allenfalls auf Zufall geschoben werden könnte, da W bis über die Hälfte von s reicht. Die Doppelwerte s1, s2 stimmen bei b ) sehr gut, bei a ) und g ) schlecht. Dies ist bei a ) nicht befremdend, da s hier fast verschwindet. Nimmt man statt dessen die Doppelwerte der größten Komponente, welche hier p ist, so findet man p = - 0,0995 und p2 = - 0,1150, was ganz leidlich stimmt.
Teilt man die ganze Reihe in zwei Fraktionen nach der Zeit, so findet man in Summa für die 4 Lagen: ×××××××××
åD (m = 10, µ= 20).
|
|
|
|
|
| 1. Frakt. | 33,10 | 25,56 | 23,18 |
| 2. - | 37,50 | 26,92 | 24,21 |
Man kann bemerken, daß die Werte sowohl von åD als c für den Zeigefinger in Reihe II und Reihe V, obgleich in derselben Weise, nur zu anderer Zeit und in anderem Zusammenhange als die Werte in dieser Reihe nach b ) gewonnen, doch sehr davon abweichen, was ein Beispiel ist, daß man Versuche, unter gleichen Umständen zu verschiedenen Zeiten angestellt, wo Übung und andere Umstände die Empfindlichkeit abgeändert haben können, und ein anderes Spiel von Zufälligkeiten stattfinden kann, nicht vergleichbar halten darf.
An sich kann es einiges Interesse haben, wenn ich hier das vollständige Verzeichnis der, in den einzelnen Versuchsfraktionen à m = 10 erhaltenen c-Werte in Reihe a beifüge, insofern man daraus ersieht, wie selbst unter Umständen, welche den konstanten Fehler möglichst verkleinern, doch der Charakter der Konstanz sich im Vorzeichen noch geltend macht. Zur Unterlage für die folgenden Berechnungen füge ich aber auch noch das Verzeichnis für die beiden anderen Reihen bei.
Werte von c in Reihe a für die einzelnen Fraktionen
à m = 10.
Mittel - 0,107 +0,096 - 0,086 +0,154c1 c2 c3 c4
- 0,22 - 0,04 - 0,02 +0,10
- 0,16 +0,08 - 0,10 +0,07
- 0,14 +0,12 - 0,03 +0,25
- 0,06 +0,21 - 0,16 +0,10
- 0,11 +0,16 - 0,20 +0,11
- 0,07 +0,07 +0,04 +0,11
- 0,20 +0,11 - 0,13 +0,16
- 0,07 +0,09 - 0,18 +0,25
- 0,04 +0,08 - 0,06 +0,18
- 0,00 +0,08 - 0,02 +0,21
Entsprechende Werte von c in Reihe b.
c1
c2
c3
c4
- 0,40 - 0,43 - 0,25
- 0,49
- 0,17 - 0,39 - 0,26
- 0,33
- 0,27 - 0,55 - 0,40
- 0,54
- 0,21 - 0,48 - 0,30
- 0,41
- 0,12 - 0,13 - 0,30
- 0,56
- 0,09 - 0,37 -
0,27 - 0,57
- 0,08 - 0,36 - 0,37
- 0,46
- 0,26 - 0,21 - 0,33 -
0,46
+0,04 - 0,25 - 0,13
- 0,14
- 0,22 - 0,49 - 0,05
- 0,26
Mittel - 0,178 - 0,366 - 0,266
- 0,422
Entsprechende Werte von c in Reihe g.
c1
c2
c3
c 4
- 0,55 - 0,24 - 0,11
- 0,19
- 0,50 - 0,27 - 0,26
- 0,30
- 0,56 - 0,38 - 0,24
+0,01
- 0,37 - 0,22 - 0,25
- 0,36
- 0,35 - 0,34 - 0,07
- 0,22
- 0,15 - 0,47 - 0,08
- 0,14
- 0,17 - 0,18 - 0,03
- ,009
- 0,39 - 0,42 - 0,12
- 0,28
- 0,04 - 0,32 +0,09
- 0,26
- 0,22 - 0,22 +0,05
- 0,33
Mittel -0,330 -0,306
-0,102 -0,216
Von der Reihe a mag auch das Verzeichnis der Fehlersummen in den einzelnen Fraktionen à m = 10 gegeben werden.
Fraktionswerte åD (m =10, µ = 1) in Reihe a.
Totalsumme19,18 16,64 15,68 19,12I U IIU I O IIO
1,64 0,56 0,88 1,60
2,12 2,12 1,00 1,10
1,48 1,88 2,22 2,60
1,60 1,90 1,96 1,60
2,12 1,20 1,00 2,52
1,70 1,50 1,80 2,32
2,00 2,34 1,70 1,72
1,84 1,50 1,40 1,90
2,08 2,44 1,88 1,84
2,60 1,20 1,84 1,92
Berechnen wir nun den wahrscheinlichen
Fehler w
des konstanten Fehlers sowohl aus åD
als aus
å (J2)
mittelst der gegebenen Formeln, indem wir µ = 10 setzen, und
für åD die in der Tabelle gegebenen
Werte zu Grunde legen, å (J
²) aber aus den Werten der vorigen Tabellen bestimmen 8).
so finden wir 9):
Werte w.
|
|
|
|
||||
|
åD |
Nach
å (J2) |
åD |
nach
å (J ²) |
nach
|
nach
å (J ²) |
|
| w1 | 0,0164 | 0,0160 | 0,0111 | 0,0270 | 0,0093 | 0,0383 |
| w2 | 0,0145 | 0,0138 | 0,0122 | 0,0285 | 0,0110 | 0,0205 |
| w3 | 0,0137 | 0,0171 | 0,0114 | 0,0226 | 0,0100 | 0,0259 |
| w4 | 0,0167 | 0,0144 | 0,0111 | 0,0299 | 0,0111 | 0,0201 |
Hier sieht man, daß bei a beide Bestimmungsweisen nahe stimmen, indes bei b und g die Bestimmungsweise nach å (J ²) mehr als doppelt so große Werte liefert, als nach åD, was ein beträchtliches Schwanken des konstanten Fehlers beweist. Die Werte W in Tabelle (s. o.) sind nach åD berechnet.
9) Die Berechnung nach åD
kommt kurz darauf zurück, den Logarithmus 0,94128 - 4 zum Logarithmus
von åDzu addieren, die Berechnung nach
å
(J ²) darauf, den Logarithmus 0,85186 -
2 zum halben Logarithmus von å (J
²) zu addieren, und beidesfalls die Zahl dazu zu nehmen.
| w1 | w2 | w3 | w4 | |
| nach å (J ²) | 0,0270 | 0,0285 | 0,0226 | 0,0299 |
| nach åJ | 0,0260 | 0,0284 | 0,0207 | 0,0303 |
Eine entsprechende Übereinstimmung findet man auch sonst immer, wonach man, da Abweichungen dieser Ordnung für den Zweck dieser Bestimmungen nicht erheblich sind, nicht nötig hätte, zu der umständlicheren Bestimmung von å (J ²) zurückzugehen, sondern sich begnügen kann, auf åJ zurückzugehen10), wenn schon prinzipiell die Bestimmung nach å (J ²) ein wenig sicherer ist.
1. Zusatz.
Herleitung der Korrektion wegen des endlichen m 11)
Die Aufgabe ist folgende: eine Reihe Fehler D
, deren Totalzahl m, ist vom arithmetischen Mittel A der
Beobachtungsgrößen an (bei den Tast- und Augenmaßversuchen
von der mittleren Fehldistanz an) gerechnet, d. h. als Differenzen der
einzelnen beobachteten Größen von A bestimmt worden,
und hat die Fehlersumme åD gegeben, worin
alle Fehler, positive und negative, nach absolutem Werte (wie positive)
verrechnet sind. Aber die, aus m Beobachtungen abgeleitete, Mittelgröße
A
ist nicht die wahre Mittelgröße V, welche aus einer unendlichen
Zahl Beobachtungen hervorgeben würde, und mithin die von der Mittelgröße
an gerechneten Fehler nicht die wahren Fehler. Die Summe der wahren Fehler
SD
soll
durch eine Korrektion aus der Summe der falschen åD
abgeleitet werden. Der Korrektionsfaktor, der sich hierbei für åD
ergibt, ist dann eben so auf den falschen Mittelfehler ![]() anwendbar.
anwendbar.
11) In Sachen S. 216 f. Vgl. Ber. d. sächs. Soc. 1861, p. 57 ff.
Nehmen wir zuerst an, die Größe V - A, um welche die wahre Mittelgröße V von der gefundenen A abweicht, sei bekannt. Sie heiße a, und man suche hiernach die Beziehung zwischen SD und åD .
a kann positiv oder negativ sein. Diesseitige falsche Fehler nun sollen solche heißen, welche mit a gleiches Vorzeichen haben, jenseitige solche, welche ungleiches Vorzeichen damit haben. Dann hat man, um åD in SD zu verwandeln 12):
1) Alle diesseitigen falschen Fehler, welche absolut größer sind, als a, deren Zahl s und deren Summe S sei, um den absoluten Wert von a zu verkleinern; gibt S - sa .
2) Alle jenseitigen falschen Fehler, deren Zahl n und deren Summe N sei, um den absoluten Wert a zu vergrößern; gibt N + na .
3) Für alle diesseitigen falschen Fehler, welche zwischen 0 und a liegen, deren Zahl z und deren Summe Z sei, die Differenz derselben von a nach absolutem Werte zu substituieren; gibt za- Z.
Also hat man:
![]() .
.
Denn die Mittelgröße der Beobachtung wird im
Mittel durch 1 Beobachtung um ![]() falsch bestimmt, folglich durch m-Beobachtungen nach bekannter Wahrscheinlichkeitsregel
um
falsch bestimmt, folglich durch m-Beobachtungen nach bekannter Wahrscheinlichkeitsregel
um ![]() falsch.
falsch.
14) Vergl. Encke im astronom. Jahrb. für 1834. S. 282 f.
Was s und Z anlangt, so kann s als die Zahl der oberhalb a auf einer Seite liegenden, d. i. positiven oder negativen, Fehler durch
![]()
gegeben angesehen werden, wenn ![]() die durch die bekannte Integraltabelle bestimmbare Wahrscheinlichkeit der
Fehler bedeutet, die nach beiden Seiten (als positive und negative) oberhalb
des absoluten Wertes a liegen. Von anderer Seite
ist
die durch die bekannte Integraltabelle bestimmbare Wahrscheinlichkeit der
Fehler bedeutet, die nach beiden Seiten (als positive und negative) oberhalb
des absoluten Wertes a liegen. Von anderer Seite
ist
![]()
wenn ![]() den wie unten zu berechnenden Bruchteil von der Totalsumme der Fehler SD
bedeutet,
welcher zwischen 0 und dem absoluten Werte a
beiderseits liegt.
den wie unten zu berechnenden Bruchteil von der Totalsumme der Fehler SD
bedeutet,
welcher zwischen 0 und dem absoluten Werte a
beiderseits liegt.
Substituieren wir diese Ausdrücke für a, s und Z, so erhalten wir
![]()
mithin, unter Substitution von
![]() für
für ![]()
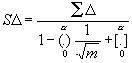
![]()
wenn e die Grundzahl der natürlichen Logarithmen, p die Ludolfsche Zahl 16).
15) Astronom. Jahrb. f. 1834, S. 305 ff.
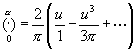
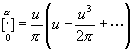
Da aber hier a= ![]() ,
so ist u =
,
so ist u = ![]() .
.
Berücksichtigt man bloß das erste Glied beider Ausdrücke, so erhält man hiernach
![]()
wofür sich mit hinreichender Approximation setzen läßt
![]() oder
oder ![]()
wovon Letzteres sich, wie man aus folgender Tabelle sieht, noch etwas mehr als Ersteres an die ganz scharfe Korrektion anschließt.
Hier folgt schließlich eine kleine Tabelle, welche
den Korrektionsfaktor von åD für
einige Werte von m sowohl nach der ganz scharfen Berechnung mit
Rückgang auf die beigefügten Werte von ![]() und
und ![]() , als
nach den verschiedenen Approximationen gibt, woraus man ersieht, daß,
selbst wenn man bis zu kleinsten Werten m herabgeht, die Korrektion
, als
nach den verschiedenen Approximationen gibt, woraus man ersieht, daß,
selbst wenn man bis zu kleinsten Werten m herabgeht, die Korrektion ![]() sich ganz unerheblich von der ganz scharfen unterscheidet, auf die, oder
auch nur auf
sich ganz unerheblich von der ganz scharfen unterscheidet, auf die, oder
auch nur auf ![]() zurückzugehen, sonach ganz überflüssig sein würde.
Zugleich ist der Korrektionsfaktor für den quadratischen mittleren
Fehler
zurückzugehen, sonach ganz überflüssig sein würde.
Zugleich ist der Korrektionsfaktor für den quadratischen mittleren
Fehler ![]() nach der schon bekannten Korrektionsweise beigefügt , woraus man sieht,
daß dieser Faktor überall größer als für åD
und mithin für
nach der schon bekannten Korrektionsweise beigefügt , woraus man sieht,
daß dieser Faktor überall größer als für åD
und mithin für ![]() ist.
ist.
|
|
|
||||||
|
|
Korr. |
|
|
||||
| 2 | 1,20000 | 1,16667 | 1,189318 | 1,183515 | 0,4273712 | 0,1471351 | 1,4142 |
| 3 | 1,12500 | 1,11111 | 1,118697 | 1,116404 | 0,3549580 | 0,1006682 | 1,2248 |
| × | |||||||
| × | |||||||
| 10 | 1,03448 | 1,03333 | 1,032889 | 1,032699 | 0,1992010 | 0,0313296 | 1,0541 |
| 20 | 1,01695 | 1,01667 | 1,016173 | 1,016139 | 0,416010 | 0,0157896 | 1,0260 |
| 30 | 1,01123 | 1,01111 | 1,010724 | 1,010702 | 0,1158224 | 0,0105573 | 1,0171 |
| × | |||||||
| 50 | 1,00671 | 1,00667 | 1,006407 | 1,006400 | 0,0898408 | 0,0063460 | 1,0101 |
| × | |||||||
| × | |||||||
| 100 | 1,00334 | 1,00333 | 1,003193 | 1,003192 | 0,0635945 | 0,0031780 | 1,0050 |
Die Werte von ![]() und
und ![]() ,
welche zur Berechnung der scharfen Korrektion gedient haben, sind, der
erstere durch Interpolation der Tabelle, welche Encke im astronom. Jahrb.
1834 gibt, mit Zuziehung der zweiten Differenzen,
,
welche zur Berechnung der scharfen Korrektion gedient haben, sind, der
erstere durch Interpolation der Tabelle, welche Encke im astronom. Jahrb.
1834 gibt, mit Zuziehung der zweiten Differenzen, ![]() aber direkt nach der (s. o.) gegebenen Formel berechnet worden.
aber direkt nach der (s. o.) gegebenen Formel berechnet worden.
2. Zusatz.17)
Herleitung der Korrektion wegen der Größe der Intervalle.
In mathematischem Sinne hat jeder Beobachtungsfehler von ganz bestimmter Größe nur eine unendlich geringe Wahrscheinlichkeit, und würde nur unendlich selten wiederkehren können. Aber bei den wirklichen Beobachtungen kann man nicht Fehler bis ins Kleinste unterscheiden, sondern nur bis zu einer gewissen Grenze damit herabgehen, und so bleibt man nach Umständen bei Zehnteilen, Hundertteilen, Tausendteilen von Linien, Graden u. dgl. in der Aufzeichnung stehen. Was dazwischen fällt, wird auf die nächstliegenden Grenzen der unterschiedenen Intervalle verlegt. Insofern man nun hierdurch. den Fehler durchschnittlich eben so oft zu groß als zu klein notiert, scheint es, daß sich dies bei einer großen Zahl Versuchen kompensieren müßte. Auch ist dies nahe aber nicht genau der Fall; vielmehr bringt der Umstand, daß die Zahl der Fehler gegebener Größe verhältnismäßig rascher als ihre Größe abnimmt, mit sich, daß hierdurch die Fehlersumme größer ausfällt, als wenn man jeden Fehler nach seinem richtigen Werte verzeichnete, und zwar in um so stärkerem Verhältnisse größer, je größer die Intervalle, die man bei der Aufzeichnung noch unterscheidet, im Verhältnisse zum mittleren Fehler sind. Denn gesetzt, man schreitet bei der Aufzeichnung durch die Intervalle 0,00; 0,10; 0,20; 0,30 etc. fort, so wird jeder Fehler z. B. über 0,15 und unter 2,5 zu 0,20 geschlagen werden; mithin die ersten Fehler zu groß, die letzten zu klein genommen werden; die Zahl der Fehler im Intervalle von 0,15 bis 0,20 ist aber um so viel größer, als die der Fehler im Intervalle von 0,20 bis 0,25, daß die Vergrößerung der Fehlersumme, welche aus ersterem Umstande erwächst, nicht durch die Verkleinerung, welche aus letzterem Umstande erwächst, kompensiert wird.
17) Vgl. Berichte d. sächs. Soc. 1861, S. 93ff. In Sachen S. 217.
So viel ich weiß, ist bis jetzt nicht untersucht worden, wie viel der hiervon abhängige Irrtum beträgt und welche Gesetze er befolgt.
Ich finde nun die oben angegebene Korrektion in folgender Weise.
Setzen wir erst, es werde wirklich jeder Fehler mit seinem wahren Werte notiert so oft, als er vorkommt, so erhalten wir durch Summierung dieser Fehler, deren Zahl m sei, die wahre Fehlersumme SD; und durch Mittelziehung daraus den wahren Mittelfehler, welcher e1 heiße. Sei hingegen i das Intervall der Einteilung, wozwischen keine Fehler angenommen werden, und beispielsweise i = 0,25 e1 oder ¼ e1,so werden alle Fehler auf die Grenzen der Intervalle von dieser Größe verlegt und eine falsche Summe åD erhalten, deren Verhältnis zur wahren SDes zu bestimmen gilt.
Nach der bekannten Tabelle des Wahrscheinlichkeitsintegrals (unter Zuziehung einer Interpolation) ist im Intervalle der Fehlergrößen von 0 bis 1/4 e1 normalerweise 0,1581058 der totalen Fehlerzahl enthalten 18). Indem diese Fehler halb zu ¼ e1, halb zu 0 geschlagen werden, wird als falsche Summe für dieses Intervall erhalten das, mit 0,1581058 m multiplizierte, Mittel zwischen 0 und 0,25 e1. Für das Intervall von 0,25 e1 bis 0,50 e1 beträgt die Normalzahl der Fehler nach der Tabelle des Integrales 0,1519585 m. Also gibt das hiermit multiplizierte Mittel zwischen 0,25 e1 und 0,50 e1 d. i. 3/8 • 0,1519585 m e1 die falsche Summe für dieses Intervall, u. s. f. durch die ganze Skala der Fehlergrößen. Die Gesamtheit dieser Summen gibt 1,003321 me1, statt der wahren Summe me1= SD.
Für ein Intervall i = e1 wurde entsprechend verfahren und dadurch der Wert
Diese Bestimmungen sind mittelst Interpolation einer bis hD19) = 3 gehenden Tabelle des Wahrscheinlichkeitsintegrales der Fehler unter Mitzuziehung der zweiten Differenzen und eigene Berechnung für höhere Werte nach Verwandlung des Integrales in eine unendliche Reihe 20) unter sorgfältiger Revision der erhaltenen Werte, gefunden.
19) h = ![]() .
.
|
|
|
|
3,0
|
0,9999779093
|
|
3,1
|
88351.
|
|
3,2
|
939740
|
|
3,3
|
969422
|
|
3,4
|
984780
|
|
3,5
|
992569
|
|
3,6
|
996441
|
|
3,7
|
998329
|
|
3,8
|
999230
|
|
3,9
|
999652
|
|
4,0
|
999846
|
|
4,1
|
999933
|
|
4,2
|
999971
|
Ohne Interpolation erhielt ich direkt
für folgende Intervallverhältnisse ![]() folgendes
Verhältnis der falschen zu der wahren Summe, wobei
folgendes
Verhältnis der falschen zu der wahren Summe, wobei ![]() =
1 ,7724539
=
1 ,7724539
|
|
|
| 0,10 |
1,0016673 |
| 0,20 |
1,0066757 |
| 0,40 |
1,026713 |
| 0,80 |
1,109193 |
Man sieht nun aus diesen wie aus den
vorigen Bestimmungen, daß der Wert, um welchen ![]() den Wert 1 übersteigt, und welcher u heiße, merklich
im Verhältnisse des Quadrates von
den Wert 1 übersteigt, und welcher u heiße, merklich
im Verhältnisse des Quadrates von![]() steht. Doch wächst der Wert etwas stärker, denn während
er bei
steht. Doch wächst der Wert etwas stärker, denn während
er bei ![]() = 0,10
= 0,10 ![]() gleich
0,0016673 ist, ist er bei
gleich
0,0016673 ist, ist er bei ![]() = 0,80
= 0,80![]() gleich
0,109193, statt daß er nach dem quadratischen Verhältnisse 0,1067072
sein sollte. Entsprechendes zeigt sich bei den Zwischenwerten. Indessen
ist die Abweichung vom quadratischen Fortschritte so gering, daß
sie füglich vernachlässigt werden kann.
gleich
0,109193, statt daß er nach dem quadratischen Verhältnisse 0,1067072
sein sollte. Entsprechendes zeigt sich bei den Zwischenwerten. Indessen
ist die Abweichung vom quadratischen Fortschritte so gering, daß
sie füglich vernachlässigt werden kann.
Heiße nun g
kurz der Wert u für ![]() =
1 , so ist nach dem quadratischen Verhältnisse
=
1 , so ist nach dem quadratischen Verhältnisse
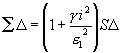
Und, sofern e der falsche, e1 der wahre Mittelfehler ist, auch
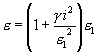
Dies führt zu der quadratischen Gleichung
e1² - ee1 + gi ² = 0
woraus
![]()
Da 4gi² immer klein gegen e2, weil g ein kleiner Bruch, so können wir vermöge Auflösung nach dem binomischen Lehrsatze und Beibehaltung der ersten beiden Glieder setzen
![]()
was gibt
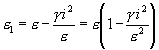
Indem aber me1 = SD , me = åD , folgt hieraus auch durch Multiplikation auf beiden Seiten mit m
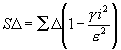
Da man mit Beobachtungsreihen, wo ![]() > 1 ist, seltener zu tun haben wird, für
> 1 ist, seltener zu tun haben wird, für ![]() < 1 aber u ein klein weniges kleiner ist, als dem Werte g
= 0,053643 nach dem quadratischen Fortschritte entspricht, so habe ich
für 0,053643 bloß 0,053 als g in
der Korrektionsformel (s. o.) angenommen.
< 1 aber u ein klein weniges kleiner ist, als dem Werte g
= 0,053643 nach dem quadratischen Fortschritte entspricht, so habe ich
für 0,053643 bloß 0,053 als g in
der Korrektionsformel (s. o.) angenommen.