l. Wenn eine gespannte Saite mit einem ganz harten, schmalen Metallstifte angeschlagen wird, der augenblicklich wieder zurückspringt, so überträgt der Stoß eine gewisse Geschwindigkeit auf die getroffene Stelle der Saite, während die ganze übrige Saite noch in Ruhe ist. Setzen wir für den Zeitmoment des Stoßes t = 0, so können wir die Bewegung der Saite durch die Bedingung bestimmen, daß im Augenblicke des Anschlages die Saite sich noch in ihrer Gleichgewichtslage befindet, und nur der getroffene Punkt eine gewisse Geschwindigkeit hat. Man setze also in den Gleichungen (l c) und (l d) Beilage III für t = 0 auch y = 0 und = 0, letzteres mit Ausnahme des geschlagenen Punktes, dessen x-Koordinate a sei. Daraus folgt

,

..............................................................(10)

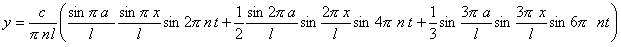
2. Etwas anders werden die Verhältnisse, wenn die Diskontinuität der Bewegung der Saite dadurch vermindert wird, daß die Hämmer mit elastischen Polstern überzogen sind, wie dies beim Pianoforte der Fall ist. Dadurch werden die höheren Obertöne merklich geschwächt, weil die Bewegung nun nicht mehr einem einzelnen Punkte, sondern einem breiteren Stück der Saite mitgeteilt wird, und auch diesem nicht in einem unteilbaren Augenblicke, wie es beim Stoße mit einem harten Körper sein würde. Vielmehr gibt das elastische Polster dem ersten Stoße nach, und dehnt sich dann wieder, so daß während der Zeit, wo der Hammer der Saite anliegt, sich die Bewegung schon über eine längere Strecke derselben ausdehnen kann. Eine genaue Analyse der Bewegung der Saite nach dem Anschlage eines Klavierhammers würde ziemlich verwickelt sein. Wenn wir aber beachten, daß die Saiten dabei verhältnismäßig wenig von der Stelle rücken, während das weiche elastische Polster der Hämmer sehr nachgiebig ist, und bedeutend zusammengepreßt werden kann, so können wir uns für die mathematische Theorie die Vereinfachung erlauben, den Druck des Hammers, welchen er gegen die Saite während des Stoßes ausübt, so groß zu setzen, als er sein würde, wenn der Hammer gegen einen ganz festen und vollkommen unnachgiebigen Körper schlüge. Demnach setzen wir den Druck des Hammers gleich

t < .

Wir müssen nun zunächst die Bewegung der Saite bestimmen während dieses Zeitabschnittes, wo der Hammer ihr anliegt, von t = 0 bis t = .

Die Saite wird während dieser Zeit von dem anliegenden Hammer in zwei Teile geteilt, deren Bewegung einzeln bestimmt werden muß. Der Wert von x für die Anschlagsstelle mag x₀ heißen¹⁾. Die Werte von y für diejenigen Teile der Saite, in denen x < x_0, bezeichnen wir mit y₁ und wo x > x₀, mit y¹. Im geschlagenen Punkte selbst muß der Druck der Saite gegen den Hammer gleich dem Drucke F sein, den dieser ausübt. Der Druck der Saite ist wie in der Gleichung (6a) Beilage IV zu berechnen, und wir erhalten daher die Gleichung:

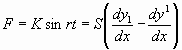......................................(11)

Von der geschlagenen Stelle gehen nach beiden Saiten Wellen aus. Es wird also y₁ die Form haben müssen

.....................................................(11a) Dies nach t integriert gibt

,

Wenn t größer als geworden ist, wird F gleich Null, und es folgt dann aus Gleichung (11 a), daß von da ab

j ' _(at) = 0also j= Const. für t > .

Um den Einfluß der Enden der Saite in passender Weise in Rechnung zu ziehen, denke man sich die Saite unendlich lang, und in allen Punkten, welche um Multipla von 2l vom Anschlagspunkte x₀ abstehen, einen ebensolchen Anschlag gleichzeitig mit dem von x₀ stattfindend, so daß von allen diesen Punkten ebensolche Wellen wie von x₀ auslaufen. Ferner denke man sich in denjenigen Punkten, in welchen x = - x₀ ± 2 a l, gleichzeitig mit dem Anschlag von x₀ einen gleichen Anschlag, aber in entgegengesetzter Richtung, erfolgend, so daß von diesen letzteren Punkten Wellen gleicher Form, aber von negativer Höhe, wie von x₀, auslaufen. Dann werden in den Endpunkten der Saite stets gleiche aber entgegengesetzte Werte der positiven und negativen Wellen zusammentreffen, diese Endpunkte also vollkommen in Ruhe bleiben, und für das wirklich existierende Stück der unendlich gedachten Saite zwischen ihren beiden Enden werden alle Bedingungen erfüllt sein, welche zu erfüllen sind.

Von dem Augenblick an, wo der Hammer die Saite verläßt, kann die Bewegung der Saite betrachtet werden als ein Ablaufen der beiden vorwärts (d. h. in Richtung der positiven x) und rückwärts (d. h. in Richtung der negativen x) fortschreitenden Wellensysteme. Von diesen Wellensystemen haben wir aber zunächst nur einzelne abgerissene Stücke gefunden, nämlich die, welche den zunächst den Anschlagspunkten gelegenen Stücken der Saite entsprechen; wir müssen die Wellen noch passend ergänzen, um ein zusammenhängendes vorwärtsschreitendes, und ein ebensolches rückwärts-schreitendes System zu erhalten.

Wenn man in Richtung der positiven x auf der Saite fortschreitet, so ist der Wert von y = 0, ehe man an eine positive rückwärtsschreitende Welle stößt; dann steigt er auf , welchen Wert er in den positiven Anschlagspunkten hat. Geht man über den Anschlagspunkt hinaus und über die von dort ans vorwärtsschreitende Welle, so findet man wieder Werte von y, die gleich Null sind, und welche bis auf  sinken, sobald man die erste negative rückwärtsschreitende Welle überschreitet. Den genannten Wert hat y im ersten negativen Anschlagspunkte. Um nun die positiven und negativen rückwärtsschreitenden Wellen mit einander zu verbinden, muß man sich zwischen jedem positiven und dem nächst folgenden negativen Anschlagspunkte die Größe + zu den Werten von y₁ hinzuaddiert denken, so daß die Wellenhöhe diesen Wert, den sie in x₀ schon hat, behält bis zu der Stelle hin, wo die entsprechende negative Welle beginnt. Hier wird also die Wellenhöhe - y₁ und sinkt bis Null. Ebenso denke man sich zwischen den negativen Anschlagspunkten und jedem nächst darauf folgenden positiven Anschlagspunkte  zur Wellenhöhe der vorwärtsschreitenden Wellen addiert. Dann sind die rückwärtsschreitenden Wellen überall positiv, die vorwärtsschreitenden überall negativ, und die Wellen sind gleichzeitig so beschaffen, daß sie bei ihrer Fortbewegung diejenige Art der Bewegung erzeugen, welche wir für die Saite gefunden haben, nachdem der Hammer sie verlassen hat.

Wir haben jetzt die Form dieser Wellensysteme als eine Summe einfacher Wellen auszudrücken. Die Wellenlänge ist 2l, weil eich die gleichartigen Anschlagspunkte in Abständen von 2l wiederholen. Nehmen wir die positiven rückwärtsschreitenden Wellen zur Zeit t = , so ist:

1) von x = 0 bis x = x₀ - ,

y₁ = 0;

2) von x = x₀ - bis x = x₀,

;

3) von x = x₀ bis 2l – x₀ -,

;

4) von x = 2l – x₀ -  bis x = 2l – x₀,

;

5) von x = 2l – x₀ bis x = 2l.

y₁ = 0.
 
 

.

+......(12)

,

.

.............(12a)

Wenn man r unendlich groß werden läßt, d. h. den Hammer vollkommen hart, so geht der Ausdruck für A_m der Gleichung (12 a) über in den von B_m in Gleichung (10).

Wenn r nicht unendlich ist, so nehmen bei steigender Größe von m die Koeffizienten A_m ab wie , bei unendlichem r wie ; bei der gerissenen Saite nahmen sie ab wie . Es entspricht dies den Theoremen, welche Stokes²⁾ über den Einfluß der Diskontinuität einer Funktion, die nach einer Fourier'schen Reihe entwickelt wird, auf die Größe der Glieder mit hoher Stellenzahl erwiesen hat. Wenn y die Funktion ist, welche entwickelt werden soll in eine Reihe

1) von der Ordnung , wenn y selbst einen plötzlichen Sprang macht;

2) von der Ordnung , wenn der Differentialquotient  einen Sprung

macht; 3) von der Ordnung , wenn erst , diskontinuierlich ist;
4) höchstens von der Ordnung e ^{- m}, Differentialquotienten der Funktion und diese selbst kontinuierlich sind.

Daraus folgt denn für die musikalischen Klänge das im Texte mehrfach erwähnte Gesetz, daß sie im Allgemeinen desto stärkere hohe Obertöne haben, je diskontinuierlicher die entsprechende Bewegung des tönenden Körpers ist.