Beilage XII.

Theorie der Kombinationstöne.
Zu Seite 262.

Es ist bekannt, daß das Prinzip von der ungestörten Superposition oszillierender Bewegungen im Allgemeinen nur so lange gilt, als die Bewegungen klein sind, so klein, daß die Bewegungskräfte, welche durch die Verschiebungen der kleinsten Teile des schwingenden Mittels gegen einander hervorgerufen werden, diesen Verschiebungen gelbst merklich proportional sind. Es läßt sich nun zeigen, daß Kombinationstöne entstehen müssen, sobald die Schwingungen so groß werden, daß auch noch das Quadrat der Verschiebungen auf die Bewegungen Einfluß erhält. Es möge für jetzt genügen, als einfachstes Beispiel die Bewegung eines einzelnen Massenpunktes unter dem Einfluß eines Wellenzuges zu betrachten, um das Resultat zu entwickeln. Nach einer ganz ähnlichen Methode lassen sich auch die Bewegungen der Luft und anderer elastischer Medien behandeln. Ein Punkt von der Masse m soll in Richtung der x-Achse oszillieren können. Die Kraft, welche ihn in seine Gleichgewichtslage zurückzuführen strebt, sei

k = ax + bx2.

Es mögen auf ihn zwei Schallwellenzüge einwirken mit der Kraft f sin (pt) und g sin (q t + c), so ist seine Bewegungsgleichung

Diese Gleichung kann man durch eine Reihe integrieren, indem man darin setzt

und die mit gleichen Potenzen von e multiplizierten Glieder einzeln gleich Null setzt, also: 1) 

2) 

3)  etc

 Aus der ersten Gleichung ergibt sich , wobei und  Es ist dies das bekannte Resultat für unendlich kleine Schwingungen, wonach der mitschwingende Körper nur seinen eigenen Ton und die ihm mitgeteilten p und q angibt. Da der Eigenton hierbei schnell verschwindet, können wir A = 0 setzen. Dann gibt die Gleichung, (2):

Dieses zweite Glied der Reihe für x enthält,wie man sieht, außer einer Konstanten, die Töne 2p, 2q, (p - q) und (p + q). Ist der Eigenton des mitschwingenden Körpers tiefer als (p + q), wie man es für das mit den Gehörknöchelchen verbundene Trommelfell des Ohres in den meisten Fällen wird voraussetzen dürfen, und sind die Intensitäten u und v nahe gleich, so wird von den einzelnen Gliedern von x2 der Ton (p - q) die größte Intensität haben; er entspricht dem bekannten tiefen Kombinationstone. Der Ton (p + q) wird viel schwächer sein, und die Töne 2p und 2q werden als schwache harmonische Obertöne der primären schwer zu hören sein.

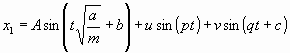Das dritte Glied der Reihe x3 enthält die Töne 3p, 3q, 2p + q, 2p - q, p + 2q, p - 2q, p und q. Von diesen ist 2p - q oder 2q - p ein Kombinationston zweiter Ordnung nach Hällstroem's Bezeichnung. Ebenso gibt das vierte Glied x4 Kombinationstöne dritter Ordnung etc.

Wenn wir nun annehmen, daß bei den Schwingungen des Paukenfells und seiner Annexa das Quadrat der Elongationen auf die Schwingungen Einfluß gewinnt, so geben die ausgeführten mechanischen Entwickelungen einen vollständigen Aufschluß über die Entstehung der Kombinationstöne. Namentlich erklärt die neue Theorie ebenso gut das Entstehen der Töne (p + q), wie der Töne (p - q), und läßt einsehen, warum bei vermehrter Intensität u und v der primären Töne die der Kombinationstöne, welche proportional uv ist, in einem schnelleren Verhältnisse steigt.

Aus der Voraussetzung über die Größe der wirkenden Kraft, welche wir oben gemacht haben:

k = a x + b x2 folgt, daß, bei einem Zeichenwechsel von x, k nicht bloß sein Zeichen, sondern auch seinen absoluten Wert ändert. Diese Annahme paßt also nur auf einen elastischen Körper, der sich gegen positive und negative Verschiebungen nicht symmetrisch verhält; nur bei einem solchen kann das Quadrat der Elongationen Einfluß auf die Bewegungen haben, und die Kombinationstöne erster Ordnung hervorrufen. Unter den im Ohre des Menschen vorhandenen schwingenden Teilen ist nun besonders das Trommelfell durch seine Asymmetrie ausgezeichnet, indem es durch den Stiel des Hammers stark nach innen gezogen ist, und ich glaube deshalb die Vermutung aufstellen zu dürfen, daß namentlich diese eigentümliche Form des Trommelfells das Entstehen der Kombinationstöne bedinge.