Analyse der Bewegung von Violinsaiten.
Zu Seite 142.
Wir wollen annehmen, daß die Linse des Vibrationsmikroskops horizontale Schwingungen ausführe, und der beobachtete Punkt vertikale, so beobachtet man Schwingungskurven, wie sie in Fig. 23, S. 140, jedoch um einen rechten Winkel gedreht, dargestellt sind. Nennen wir die vertikalen Ordinaten y, die horizontalen x, so ist y direkt proportional den Elongationen des schwingenden Punktes, x denen der schwingenden Linse. Letztere macht eine einfache pendelartige Bewegung; ist die Zahl ihrer Schwingungen also n, und t die Zeit, so ist im Allgemeinen
Wenn nun y auch n Schwingungen macht, so sind x und y beide periodisch, und haben dieselbe Dauer der Periode; nach Ablauf jeder einzelnen solchen Periode haben alsdann x und y wieder die gleichen Werte, und der beobachtete Punkt befindet sich alsdann wieder genau an demselben Orte, wo er im Anfang der Periode war. Dies gilt für jeden Punkt der Kurve und für jede neue Wiederholung der schwingenden Bewegung, so daß die Kurve feststehend erscheint.
Denkt man eine Schwingungskurve von der Art, wie sie in den früheren Figuren 5, 6, 7, 8, 9, 10 Seite 33 bis 38 dargestellt sind, und deren horizontale Abszissen der Zeit direkt proportional sind, um einen Zylinder gewickelt, dessen Umfang gleich der Länge einer Perlode jener Kurven ist, so daß nun die Zeit t längs des Zylinderumfanges zu messen ist, und nennt man x die Entfernungen von einer durch die Achse des Zylinders gelegten Ebene, so ist auch hier
Haben x und y nicht genau dieselbe Periode, macht z. B. y n Schwingungen, x aber n + Dn, wo unter Dn eine sehr kleine Größe verstanden ist, so kann man den Ausdruck für x schreiben:
Da eine Größe, welche nach der Periode p periodisch ist, auch betrachtet werden kann als periodisch nach 2p oder 3p oder ap, wenn a eine beliebige ganze Zahl ist, so passen diese Betrachtungen auch für den Fall, wo die Periode von y ein aliquoter Teil der Periode von x ist, oder umgekehrt, oder beide aliquote Teile derselben dritten Periode sind, d. h. für den Fall, wenn die Töne der Stimmgabel und des beobachteten Körpers in irgend einem konsonanten Verhältnisse stehen; nur muß die gemeinsame Schwingungsperiode nicht so lang sein, daß während derselben der Lichteindruck im Auge erlöschen könnte.
Aus den beobachteten Kurven Fig. 23 B, C und Fig. 24 folgt, daß alle Saitenpunkte abwechselnd auf- und absteigen in der Weise, daß das Aufsteigen mit konstanter Geschwindigkeit geschieht, und das Absteigen ebenso mit einer konstanten Geschwindigkeit, deren Wert aber von der Geschwindigkeit des Aufsteigens verschieden sein kann. Wenn der Bögen in einem Knotenpunkte eines der höheren Obertöne die Saite angreift, so geht in allen Knotenpunkten desselben Tones die Bewegung ganz rein in der beschriebenen Weise vor sich. In anderen Punkten der Saite sind noch kleine Kräuselungen der Schwingungsfigur erkennbar die aber doch das Bild der beschriebenen Hauptbewegung deutlich erkennen lassen.
Rechnen wir die Zeit in Fig.
62 von der Abszisse des Punktes a
ab, so daß für at = 0, setzen
wir ferner für den Punkt bt = ![]() ,
und für den Punkt g t = T, so daß
letzteres die Dauer einer ganzen Periode bezeichnet, dann ist der Wert
von y zu setzen:
,
und für den Punkt g t = T, so daß
letzteres die Dauer einer ganzen Periode bezeichnet, dann ist der Wert
von y zu setzen:
von t = ![]() .
bis t = T y = g (T — t)
+ h......................................(1)
.
bis t = T y = g (T — t)
+ h......................................(1)
![]()
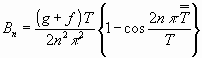
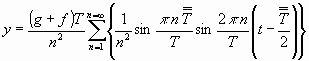 .........................(2)
.........................(2)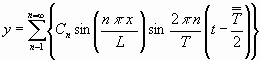
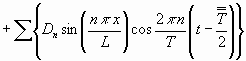 ....................................(3)
....................................(3)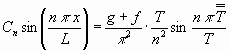 .........................................(3a)
.........................................(3a)
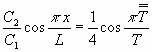 .
.![]() ....................................................................................(3b)
....................................................................................(3b)
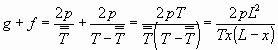
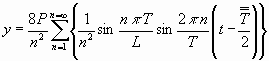 ...........................(3c)
...........................(3c)Setzt man ![]() ==
0, so wird y für jeden Werth von x gleich Null, also
gehen alle Teile der Saite gleichzeitig durch die Gleichgewichtslage der
Saite. Von da ab ist die Geschwindigkeit f des Punktes
x
==
0, so wird y für jeden Werth von x gleich Null, also
gehen alle Teile der Saite gleichzeitig durch die Gleichgewichtslage der
Saite. Von da ab ist die Geschwindigkeit f des Punktes
x
![]() ................................................................(4a)
................................................................(4a)
L t = x T.
Die kleinen Kräuselungen der Schwingungsfiguren, welche so oft beobachtet werden, ergeben sich wohl meist daraus, daß diejenigen Töne, welche an der gestrichenen Stelle oder in deren nächster Nähe Knotenpunkte haben, und deshalb vom Bogen gar nicht oder nur schwach angeregt werden können, gedämpft werden und wegfallen. Wenn der Bogen in einem dem Stege benachbarten Knotenpunkte des mten Obertones streicht, so haben die Schwingungen dieses mten, ferner des 2mten, des 3mten etc. Tones gar keinen Einfluß auf die Bewegung des vom Bogen berührten Punktes der Saite, und sie können deshalb wegfallen, ohne daß die Wirkung des Bogens auf die Saite geändert wird, und in der Tat erklären sich daraus die beobachteten Kräuselungen der Schwingungsfigur. Was in dem Falle geschieht, wo der Bogen die Saite zwischen je zwei Knotenpunkten angreift, habe ich nicht durch Beobachtung ermitteln können.