Beilage IX.
Phasen der durch Resonanz entstandenen Wellen.
Zu Seite 202.
Es sei eine Stimmgabel der Mündung einer Resonanzröhre genähert,
und das Ohr des Hörenden befinde sich in einer gegen die Dimensionen
der Öffnung sehr großen Entfernung von der Röhre. Ich habe
bewiesen1), daß wenn ein tönender Punkt sich im Punkte
B
eines teilweise von festen Wänden begrenzten, teilweise unbegrenzten
Raumes befindet, die Schallbewegung in einem anderen Punkte
A desselben
Raumes der Intensität und Phase nach dieselbe ist, als sie in B
sein würde, wenn sich der tönende Punkt in
A befände.
B sei der Ort der Stimmgabel (oder genauer des Endes einer ihrer
Zinken), A der des Ohres. Die Bewegung der Luft, welche eintritt,
wenn sich die Stimmgabel nahe vor der Öffnung befindet, läßt
sich nicht wohl bestimmen, wohl aber habe ich (S. 47 und 48 der zitierten
Abhandlung) die Bewegung bestimmt für den Fall, wo die Stimmgabel
in großer Entfernung ist. Denken wir uns also die Gabel an den Ort
des Ohres nach A gebracht, so haben wir die Schallbewegung an dem
Punkte B nahe der Mündung zu bestimmen. Diese Schallbewegung
ist aus zwei Teilen zusammengesetzt, der eine Teil, dessen Potential dort
mit Fbezeichnet ist, entspricht der Bewegung,
welche auch bei geschlossener Mündung der Resonanzröhre vorhanden
sein würde, und ist in dem vorliegenden Falle zu klein, um wahrgenommen
zu werden; der andere Teil, mit Y bezeichnet,
hat nach den dort angewendeten Bezeichnungen im freien Raume und in einiger
Entfernung von der Öffnung den Wert [S. 38 Gleichung (12h)]:
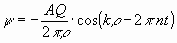 ..............................................................(1)
(Q der Querschnitt der Röhre, r
die Entfernung vom Mittelpunkt ihrer Öffnung, n die Schwingungszahl,
..............................................................(1)
(Q der Querschnitt der Röhre, r
die Entfernung vom Mittelpunkt ihrer Öffnung, n die Schwingungszahl, 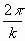 die Wellenlänge). Die Bewegung in unendlich kleiner Entfernung r
vom tönenden Punkte A ist gegeben durch die Gleichung:
die Wellenlänge). Die Bewegung in unendlich kleiner Entfernung r
vom tönenden Punkte A ist gegeben durch die Gleichung:
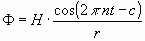 ......................................................................(2)
und es ist, wenn wir unter r1 die Entfernung des imaginären
tönenden Punktes A vom Mittelpunkt der Röhrenmündung
verstehen, nach (16c) und (13a) der zitierten Abhandlung:
......................................................................(2)
und es ist, wenn wir unter r1 die Entfernung des imaginären
tönenden Punktes A vom Mittelpunkt der Röhrenmündung
verstehen, nach (16c) und (13a) der zitierten Abhandlung:
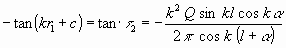 .................................(2a)
(l Länge der Röhre, a eine
Konstante, die von der Form ihrer Mündung abhängt) und endlich
ist (16c, 13a) die dort I genannte Größe:
.................................(2a)
(l Länge der Röhre, a eine
Konstante, die von der Form ihrer Mündung abhängt) und endlich
ist (16c, 13a) die dort I genannte Größe:
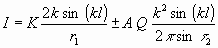 woraus
folgt
woraus
folgt
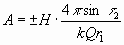 ..................................................(3)
..................................................(3)
1) Journal für reine und angewandte Mathematik, Bd.
LVII, S. l bis 72. Wiss. Abh. Bd. I, S. 303 bis 382. Theorie der Luftschwingungen
in Röhren mit offenen Enden. §. 5.
Das ± Zeichen werde so bestimmt, daß
die Konstanten A und H gleiches Zeichen bekommen,
dann muß t2 zwischen 0 und
p liegen.
Hier ist die Stärke der Resonanz A ausgedrückt durch
die Intensität des tönenden Punktes H, den Querschnitt
der Resonanzröhre Q, die Entfernung r1 des
tönenden Punktes von deren Mündung und die Größe
r2.
Der Phasenunterschied zwischen den Punkten
A und B ist nach
Gleichung (l), (2) und (2 a):
p - kr +
c = p - kr - kr1
- t2.
Die Grosse krkann aber bei den
Entfernungen des Punktes B von der Mitte der Öffnung, die wir
anwenden können, als verschwindend klein betrachtet werden, so daß
bei der Schwächung des Tons, die wir durch Entfernung der Stimmgabel
von der Mündung der Röhre erreichen, die Phase nicht merklich
geändert wird. Wenn wir dagegen die Stimmung der Röhre verändern,
so wird in dem Ausdruck für die Phase nur die Größe
t2,
welche von kl nach Gleichung (2a) abhängig ist, geändert,
und dem entspricht immer auch eine Änderung in der Stärke der
Resonanz, da in deren Ausdruck in Gleichung (3) sin t2
als Faktor vorkommt. Die stärkste Resonanz tritt ein, wenn sin t2
= 1, also t2 =  .
Nennen wir dies Maximum der Resonanz A, so ist
.
Nennen wir dies Maximum der Resonanz A, so ist
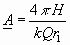 ,
und für andere Abstimmungen der Röhre, falls deren Querschnitt
nicht geändert wird,
,
und für andere Abstimmungen der Röhre, falls deren Querschnitt
nicht geändert wird,
 .
Ob der Winkel t2 kleiner oder größer
als ein Rechter zu nehmen ist, bestimmt sich darnach, ob in Gleichung (2a)
der Wert von
.
Ob der Winkel t2 kleiner oder größer
als ein Rechter zu nehmen ist, bestimmt sich darnach, ob in Gleichung (2a)
der Wert von
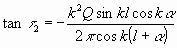 positiv oder negativ ist. Da nun k, Q und cos k
astets
positiv sind, so hängt der Wert von tan t2
ab von dem Faktor
positiv oder negativ ist. Da nun k, Q und cos k
astets
positiv sind, so hängt der Wert von tan t2
ab von dem Faktor 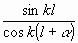 .
Wenn cos k (l + a) = 0, findet
Maximum der Resonanz statt: wenn sin kl = 0, ein Minimum. Es ist
also t2 <
.
Wenn cos k (l + a) = 0, findet
Maximum der Resonanz statt: wenn sin kl = 0, ein Minimum. Es ist
also t2 < 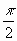 ,
wenn man durch Verlängerung der Röhre sich einem Minimum der
Resonanz nähert, dagegen t2
>
,
wenn man durch Verlängerung der Röhre sich einem Minimum der
Resonanz nähert, dagegen t2
> 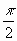 wenn
man sich einem Maximum nähert. Bei den Anwendungen ist die Röhre
immer nahe einem Maximum der Resonanz, und also <
wenn
man sich einem Maximum nähert. Bei den Anwendungen ist die Röhre
immer nahe einem Maximum der Resonanz, und also < 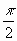 ,
wenn die Röhre zu tief, und t2
>
,
wenn die Röhre zu tief, und t2
> 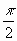 , wenn
die Röhre zu hoch gestimmt ist.
, wenn
die Röhre zu hoch gestimmt ist.
Macht man durch Verstimmung der Röhre A2 = ½
A2,
so ist die Veränderung der Schwingungsphase ==  .
So kann man also die eingetretene Veränderung der Phase immer nach
der Veränderung in der Stärke der Resonanz wenigstens abschätzen.
.
So kann man also die eingetretene Veränderung der Phase immer nach
der Veränderung in der Stärke der Resonanz wenigstens abschätzen.
Ein ähnliches Gesetz findet statt für die Phasen der schwingenden
Stimmgabeln verglichen mit denen des erregenden Stromes. Um die Betrachtung
zu vereinfachen, will ich hier nur einen einzelnen schwingenden Massenpunkt
betrachten, der durch eine elastische Kraft immer wieder in seine Gleichgewichtslage
zurückgeführt wird. Wenn x die Entfernung des Massenpunktes
aus seiner Gleichgewichtslage ist, sei — a2x die
elastische Kraft. Es wirke ferner eine periodische Kraft ein, wie sie in
unseren Versuchen durch die elektrischen Ströme hervorgebracht wird,
deren Größe sei A sin nt, und eine die Schwingungen dämpfende
Kraft, deren Größe der Geschwindigkeit proportional ist, also
gleich 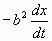 .
Eine solche entsteht bei unseren Versuchen teils durch die Reibung und
den Luftwiderstand, namentlich aber durch die von der bewegten Stimmgabel
induzierten Ströme, welche am meisten dazu beitragen, die Schwingungen
zu dämpfen. Ist m die Masse des schwingenden Punktes, so ist
also
.
Eine solche entsteht bei unseren Versuchen teils durch die Reibung und
den Luftwiderstand, namentlich aber durch die von der bewegten Stimmgabel
induzierten Ströme, welche am meisten dazu beitragen, die Schwingungen
zu dämpfen. Ist m die Masse des schwingenden Punktes, so ist
also
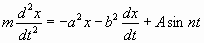 ................................................(4)
Das vollständige Integral dieser Gleichung ist
................................................(4)
Das vollständige Integral dieser Gleichung ist
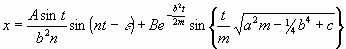 ............(4a)
worin
............(4a)
worin
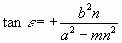 ....................................................................(4b)
Das mit B multiplizierte Glied in der Gleichung (4a) ist
nur im Anfange der Bewegung von Einfluß; wegen des Faktors
....................................................................(4b)
Das mit B multiplizierte Glied in der Gleichung (4a) ist
nur im Anfange der Bewegung von Einfluß; wegen des Faktors 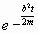 wird es bei wachsender Zeit t immer kleiner und kleiner,
so daß es schließlich verschwindet. Seine Existenz im Anfange
der Bewegung ist aber Schuld daran, daß die in Beilage
VIII erwähnten vorübergehenden Schwebungen entstehen,
wenn die Größe n wenig verschieden ist von
wird es bei wachsender Zeit t immer kleiner und kleiner,
so daß es schließlich verschwindet. Seine Existenz im Anfange
der Bewegung ist aber Schuld daran, daß die in Beilage
VIII erwähnten vorübergehenden Schwebungen entstehen,
wenn die Größe n wenig verschieden ist von
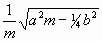 .
Das mit A multiplizierte Glied der Gleichung (4a) entspricht
dagegen der dauernden Schwingung des Massenpunktes. Die lebendige Kraft
i2
dieser Bewegung ist gleich dem Maximalwerte von
.
Das mit A multiplizierte Glied der Gleichung (4a) entspricht
dagegen der dauernden Schwingung des Massenpunktes. Die lebendige Kraft
i2
dieser Bewegung ist gleich dem Maximalwerte von 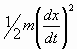 ,
nämlich:
,
nämlich:
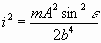 .......................................................................(5)
Wenn man nun die Tonhöhe des erregenden Tones, d. h. n sich
verändern läßt, so erreicht i2 seinen
Maximalwert, den wir mit I2 bezeichnen wollen, wenn
sin2 e = l oder tan e
= ± ¥
,
wobei
.......................................................................(5)
Wenn man nun die Tonhöhe des erregenden Tones, d. h. n sich
verändern läßt, so erreicht i2 seinen
Maximalwert, den wir mit I2 bezeichnen wollen, wenn
sin2 e = l oder tan e
= ± ¥
,
wobei
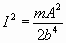 Wir können deshalb auch schreiben:
i 2 = I 2 sin2 e
..........…………………………..... (5a)
Dieselbe Größe e bestimmt also in
Gleichung (4a) den Phasenunterschied zwischen den periodisch wechselnden
Elongationen x der Masse und den wechselnden Werten der Kraft, sowie
in Gleichung (5a) die Stärke der Resonanz.
Wir können deshalb auch schreiben:
i 2 = I 2 sin2 e
..........…………………………..... (5a)
Dieselbe Größe e bestimmt also in
Gleichung (4a) den Phasenunterschied zwischen den periodisch wechselnden
Elongationen x der Masse und den wechselnden Werten der Kraft, sowie
in Gleichung (5a) die Stärke der Resonanz.
Die Bedingung, daß tan e = ±¥
sei, wird nach (4b) erfüllt, wenn
a2 = m n2.
Bezeichnen wir also den Wert von n, welcher dem Maximum des Mitschwingens
entspricht, mit N, so ist
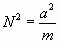 ....................................................................................(5b)
Dieser Ton stärkster Resonanz ist gleich dem Tone, welchen
der betreffende Massenpunkt geben würde, wenn er nur unter dem Einfluß
der elastischen Kraft ohne Reibung und ohne fremde Erregung in Schwingung
gesetzt wäre. Davon ist etwas verschieden der Eigenton des Körpers,
den er unter Einfluß der Reibung und des Luftwiderstandes gibt, dessen
Tonhöhe v in dem zweiten Gliede der Gleichung (4a) gegeben
ist:
....................................................................................(5b)
Dieser Ton stärkster Resonanz ist gleich dem Tone, welchen
der betreffende Massenpunkt geben würde, wenn er nur unter dem Einfluß
der elastischen Kraft ohne Reibung und ohne fremde Erregung in Schwingung
gesetzt wäre. Davon ist etwas verschieden der Eigenton des Körpers,
den er unter Einfluß der Reibung und des Luftwiderstandes gibt, dessen
Tonhöhe v in dem zweiten Gliede der Gleichung (4a) gegeben
ist:
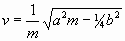 .
Erst wenn b = 0 gesetzt wird, d. h. Reibung und Luftwiderstand verschwinden,
wird
.
Erst wenn b = 0 gesetzt wird, d. h. Reibung und Luftwiderstand verschwinden,
wird
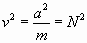 .
Nun ist in allen praktischen Fällen, wo wir das Phänomen des
Mitschwingens beobachten, b verschwindend klein, so daß der
Unterschied zwischen dem Tone stärkster Resonanz und dem Eigentone
der schwingenden Körper vernachlässigt werden kann, wie dies
auch im Texte geschehen ist. Es wird unter Einführung der Größe
N
die Gleichung (4b)
.
Nun ist in allen praktischen Fällen, wo wir das Phänomen des
Mitschwingens beobachten, b verschwindend klein, so daß der
Unterschied zwischen dem Tone stärkster Resonanz und dem Eigentone
der schwingenden Körper vernachlässigt werden kann, wie dies
auch im Texte geschehen ist. Es wird unter Einführung der Größe
N
die Gleichung (4b)
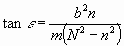 ................................................................(4c)
Wegen der auf Seite 248 erörterten Frage, wie die Membrana basilaris
des Ohrs bei Geräuschen bewegt wird, interessiert uns noch das Integral
einer Gleichung, in welcher an Stelle des A sin (nt)
der Gleichung (4) eine willkürliche Funktion der Zeit yt,
tritt. Man kann eine solche allerdings, wenn sie für sehr große
positive und negative Werte der Zeit gleich Null wird, mittels des Fourier'schen
Integrals auch in eine Summe (Integral) von Gliedern A sin (n t + c)
verwandeln, und dann für jedes einzelne dieser Glieder die eben gefundene
Lösung anwenden und schließlich wieder die Summe aller dieser
Lösungen bilden. Aber diese Form der Lösung wird unübersichtlich,
weil sie eine kontinuierliche Reihe von Tönen anzeigt, deren jeder
von t = - ¥ bis t = + ¥
besteht. Wir müssen also einen andern Weg einschlagen.
................................................................(4c)
Wegen der auf Seite 248 erörterten Frage, wie die Membrana basilaris
des Ohrs bei Geräuschen bewegt wird, interessiert uns noch das Integral
einer Gleichung, in welcher an Stelle des A sin (nt)
der Gleichung (4) eine willkürliche Funktion der Zeit yt,
tritt. Man kann eine solche allerdings, wenn sie für sehr große
positive und negative Werte der Zeit gleich Null wird, mittels des Fourier'schen
Integrals auch in eine Summe (Integral) von Gliedern A sin (n t + c)
verwandeln, und dann für jedes einzelne dieser Glieder die eben gefundene
Lösung anwenden und schließlich wieder die Summe aller dieser
Lösungen bilden. Aber diese Form der Lösung wird unübersichtlich,
weil sie eine kontinuierliche Reihe von Tönen anzeigt, deren jeder
von t = - ¥ bis t = + ¥
besteht. Wir müssen also einen andern Weg einschlagen.
Die zu integrierende Differentialgleichung ist:
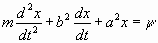 .............................................................(5)
worin x die gesuchte, y die gegebene
Funktion der Zeit ist, letztere für jeden Wert von t als endlich
vorausgesetzt.
.............................................................(5)
worin x die gesuchte, y die gegebene
Funktion der Zeit ist, letztere für jeden Wert von t als endlich
vorausgesetzt.
Setze
 ............................................................(6)
worin c eine Wurzel der Gleichung bezeichnet:
............................................................(6)
worin c eine Wurzel der Gleichung bezeichnet:
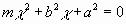 ....................................................................(6a)
das heißt
....................................................................(6a)
das heißt
 ...........................................................(6b)
was wir bezeichnen wollen als
...........................................................(6b)
was wir bezeichnen wollen als
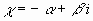 ,
indem wir den Koeffizienten der Dämpfung als klein genug annehmen,
daß die Wurzelgröße, die wir mit ß bezeichnet
haben, reell sei.
,
indem wir den Koeffizienten der Dämpfung als klein genug annehmen,
daß die Wurzelgröße, die wir mit ß bezeichnet
haben, reell sei.
Es ist alsdann, wenn y eine kontinuierliche
Funktion ist
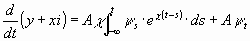 ......................................(6c)
......................................(6c)
 ..................(6d)
..................(6d)
Multipliziert man (6) mit a2, (6c) mit b2,
(6d) mit m und addiert, so erhält man mit Berücksichtigung
von (6a) folgende Gleichung zwischen, den imaginären Teilen der betreffenden
Ausdrücke:
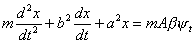 Setzen wir also
Setzen wir also
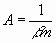 ,
so ergibt Gleichung (6) einen Wert von x, der der Differentialgleichung
(5) genügt, und für jeden Wert der Zeit endlich ist, nämlich
,
so ergibt Gleichung (6) einen Wert von x, der der Differentialgleichung
(5) genügt, und für jeden Wert der Zeit endlich ist, nämlich
 Das heißt x erscheint als eine Summe von superponierten
erlöschenden Oszillationen, deren Anfangszeit s und
deren Anfangsamplitude der Wert
Das heißt x erscheint als eine Summe von superponierten
erlöschenden Oszillationen, deren Anfangszeit s und
deren Anfangsamplitude der Wert 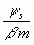 ist;
und zwar gibt jeder dem Augenblick t vorausgegangene Augenblick
seinen Beitrag. Dieser Beitrag verschwindet aber für diejenigen Teile
der Bewegung, welche längere Zeit vor dem betrachteten Augenblick
erregt worden sind, d. h. für die, bei denen der Exponent a
(t
- s) eine große Zahl ist, und die Bewegung hängt also in
jedem Augenblick nur ab von denjenigen Kräften y,
die kurz vorher eingewirkt haben.
ist;
und zwar gibt jeder dem Augenblick t vorausgegangene Augenblick
seinen Beitrag. Dieser Beitrag verschwindet aber für diejenigen Teile
der Bewegung, welche längere Zeit vor dem betrachteten Augenblick
erregt worden sind, d. h. für die, bei denen der Exponent a
(t
- s) eine große Zahl ist, und die Bewegung hängt also in
jedem Augenblick nur ab von denjenigen Kräften y,
die kurz vorher eingewirkt haben.
Findet die Einwirkung der Kraft y nur während
einer begrenzten Zeit von t0 bis t1
statt, so wird das x der Gleichung (6d) erst bis zur Zeit
t0
gleich Null sein, dann von Null verschieden werden, und nach
t1 wird die Bewegung die einfach erlöschender Schwingungen.
Übrigens wird die Größe von x davon abhängen,
wie oft große positive Werte von y mit
großen positiven von sin(bt) zusammentreffen
und negative mit negativen. Der Wert von x wird verhältnismäßig
am größten werden, wenn y und sin(bt)
ihr Zeichen nahehin gleichzeitig wechseln.
Hat yt, von der Zeit t
= t0 zur Zeit t = t1 einen konstanten
Wert p gehabt, so wird
 ,
wenn man setzt
k cos h = - a
,
wenn man setzt
k cos h = - a
k sin h = b
ferner
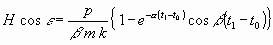
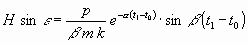 .
.
Wählt man für k den positiven Wert von 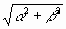 ,
wird h ein stumpfer Winkel. Gibt man dem H
das Vorzeichen des Druckes p, so hat der zwischen +
,
wird h ein stumpfer Winkel. Gibt man dem H
das Vorzeichen des Druckes p, so hat der zwischen +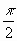 und -
und - 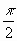 zunehmende Winkel e dasselbe Vorzeichen wie
sin b (t1 — t0).
Der Ausdruck für x stellt dann erlöschende Schwingungen
dar, deren Anfangsamplitude, wenn wir die Dauer der Einwirkung t1
- t0 = tsetzen, den
Wert hat
zunehmende Winkel e dasselbe Vorzeichen wie
sin b (t1 — t0).
Der Ausdruck für x stellt dann erlöschende Schwingungen
dar, deren Anfangsamplitude, wenn wir die Dauer der Einwirkung t1
- t0 = tsetzen, den
Wert hat
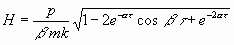 ,
Dies ist für verschiedene Werte von t ein
Maximum, wenn cos (bt+ h)
= cos h × e-at,
oder für kleine Werte von a und t
, wenn bt annähernd eine ungerade Anzahl
halber Schwingungsperioden des Eigentons umfaßt; für eine gerade
Anzahl solcher Perioden dagegen ist H ein Minimum.
,
Dies ist für verschiedene Werte von t ein
Maximum, wenn cos (bt+ h)
= cos h × e-at,
oder für kleine Werte von a und t
, wenn bt annähernd eine ungerade Anzahl
halber Schwingungsperioden des Eigentons umfaßt; für eine gerade
Anzahl solcher Perioden dagegen ist H ein Minimum.
Nach lange fortgesetzter Einwirkung der Kraft p aber verschwinden
die Exponentialfunktionen und H bekommt den konstanten Wert
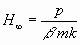 .
Für sehr kleine Werte von t dagegen können
die Anfangsmaxima für bt= pden
Wert erreichen
.
Für sehr kleine Werte von t dagegen können
die Anfangsmaxima für bt= pden
Wert erreichen
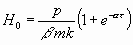 .
Wenn der Druck p sein Zeichen wechselt, so oft cos (bt
) es tut, so wird die Amplitude
H nach n
solchen Zeichenwechseln
.
Wenn der Druck p sein Zeichen wechselt, so oft cos (bt
) es tut, so wird die Amplitude
H nach n
solchen Zeichenwechseln
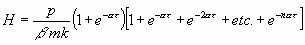 oder
oder
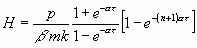 .
Dieser Ausdruck zeigt die mit jedem Zeichenwechsel wachsende Verstärkung
an, welche bei Übereinstimmung der Periode des Druckwechsels mit der
Periode des Eigentons eintritt. Der Nenner (l – e -at)
gibt die Größe der Dämpfung während einer halben Schwingungsperiode.
Wenn diese sehr klein ist, so wird H schließlich sehr groß,
endlich nach unendlich vielen Wiederholungen
.
Dieser Ausdruck zeigt die mit jedem Zeichenwechsel wachsende Verstärkung
an, welche bei Übereinstimmung der Periode des Druckwechsels mit der
Periode des Eigentons eintritt. Der Nenner (l – e -at)
gibt die Größe der Dämpfung während einer halben Schwingungsperiode.
Wenn diese sehr klein ist, so wird H schließlich sehr groß,
endlich nach unendlich vielen Wiederholungen
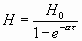 .
.
![]() ..................................................(3)
..................................................(3)
![]() .
So kann man also die eingetretene Veränderung der Phase immer nach
der Veränderung in der Stärke der Resonanz wenigstens abschätzen.
.
So kann man also die eingetretene Veränderung der Phase immer nach
der Veränderung in der Stärke der Resonanz wenigstens abschätzen.
![]() .
Eine solche entsteht bei unseren Versuchen teils durch die Reibung und
den Luftwiderstand, namentlich aber durch die von der bewegten Stimmgabel
induzierten Ströme, welche am meisten dazu beitragen, die Schwingungen
zu dämpfen. Ist m die Masse des schwingenden Punktes, so ist
also
.
Eine solche entsteht bei unseren Versuchen teils durch die Reibung und
den Luftwiderstand, namentlich aber durch die von der bewegten Stimmgabel
induzierten Ströme, welche am meisten dazu beitragen, die Schwingungen
zu dämpfen. Ist m die Masse des schwingenden Punktes, so ist
also
![]() ..................(6d)
..................(6d)
![]() .
.