Beilage XV.
Berechnung der Intensität der Schwebungen verschiedener
Intervalle.
Zu Seite 312 und 318.
Wir benutzen wieder die in der Beilage
IX unter (4a), (4b), (6) und (5a) entwickelten Formeln für
die Stärke des Mitschwingens. Es sei für den Ton stärkster
Resonanz eines Corti'schen Elementarorgans n die Anzahl der Schwingungen
in 2pSekunden, n1 und n2
seien die entsprechenden Schwingungszahlen für zwei gehörte Töne
und B1 sowie B2 die Geschwindigkeitsmaxima
der Schwingungen, welche sie in den gleichgestimmten Corti'schen Organen
hervorbringen, so sind die Geschwindigkeitsmaxima B1
und B2, welche beide in. dem Gebilde von der Schwingungszahl
n
hervorbringen, nach Gleichung (5a) Beilage
IX:
B1 = B1 sin e1
B2 = B2 sin e2
worin:
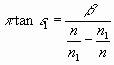 und
und 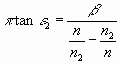 Darin ist b eine Größe, welche wir
als unabhängig von n betrachten können. Die Intensität
der Schwingungen des Organs von der Schwingungszahl n schwankt demnach,
wenn beide Töne n1 und n2 zusammenwirken,
zwischen den Werten:
(B1 + B2 )2 und (B1
- B2.)2
Der Unterschied beider Größen, welcher die Stärke der Schwebungen
mißt, ist:
4 B1 B2 = 4 B1B2
sin e1 sin e2
................................................ (7)
Bei gleichen Unterschieden in der Stimmung ist die Stärke der Schwebungen
also abhängig von dem Produkte B1B2.
Für den mten Oberton eines Violinklanges können wir
Darin ist b eine Größe, welche wir
als unabhängig von n betrachten können. Die Intensität
der Schwingungen des Organs von der Schwingungszahl n schwankt demnach,
wenn beide Töne n1 und n2 zusammenwirken,
zwischen den Werten:
(B1 + B2 )2 und (B1
- B2.)2
Der Unterschied beider Größen, welcher die Stärke der Schwebungen
mißt, ist:
4 B1 B2 = 4 B1B2
sin e1 sin e2
................................................ (7)
Bei gleichen Unterschieden in der Stimmung ist die Stärke der Schwebungen
also abhängig von dem Produkte B1B2.
Für den mten Oberton eines Violinklanges können wir 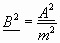 setzen, nach Beilage VI,
und wenn also der m1te und m2te Oberton
zweier Violinklänge Schwebungen geben, setzen wir die Intensität
ihrer Schwebungen bei gleichen Intervalldifferenzen gleich
setzen, nach Beilage VI,
und wenn also der m1te und m2te Oberton
zweier Violinklänge Schwebungen geben, setzen wir die Intensität
ihrer Schwebungen bei gleichen Intervalldifferenzen gleich
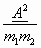 Dieser Ausdruck ist der Berechnung der letzten Spalte der Tabelle auf S.
313 zu Grunde gelegt worden.
Dieser Ausdruck ist der Berechnung der letzten Spalte der Tabelle auf S.
313 zu Grunde gelegt worden.
Für die auf Seite 318 und 319 besprochene Berechnung der Rauhigkeit
verschiedener Intervalle führen wir noch folgende abkürzende
Bezeichnungen ein;
n1 + n2 = 2 N,
n1 = N (1 + d),
n2 = N (1 - d),
n = N (l + v ).
Dann ist
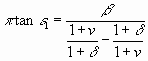 ,
, 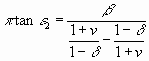 Da kräftiges Mitschwingen nur stattfindet, wenn v und
d
sehr klein sind, so kann man annähernd setzen:
Da kräftiges Mitschwingen nur stattfindet, wenn v und
d
sehr klein sind, so kann man annähernd setzen:
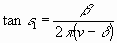 ,
, 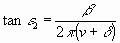 Diese Werte in Gleichung (7) eingesetzt ergeben:
Diese Werte in Gleichung (7) eingesetzt ergeben:
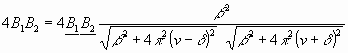 .................(7a)
Wenn wir nun v, d. h. die Tonhöhe des mitschwingenden Corti'schen
Organs, als veränderlich betrachten, erreicht der Wert von 4B1B2
sein Maximum, wenn v = 0, also n = N = 1/2
(n1 + n2); und der Wert dieses Maximum
selbst, den wir mit s bezeichnen wollen, ist:
.................(7a)
Wenn wir nun v, d. h. die Tonhöhe des mitschwingenden Corti'schen
Organs, als veränderlich betrachten, erreicht der Wert von 4B1B2
sein Maximum, wenn v = 0, also n = N = 1/2
(n1 + n2); und der Wert dieses Maximum
selbst, den wir mit s bezeichnen wollen, ist:
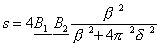 ....................................................................(7b)
Ich habe mich bei Berechnung des Grades der Rauhigkeit, welche der Zusammenklang
zweier Töne gibt, die um das Intervall 2dvon
einander entfernt sind, damit begnügt den hier gefundenen Maximalwert
der Schwebungen zu berücksichtigen, welcher in dem am günstigsten
gelegenen Corti'schen Organe stattfindet. Allerdings werden schwächere
Schwebungen auch noch in den benachbarten Faserbögen erzeugt, aber
in schnell abnehmender Intensität. Es könnte deshalb vielleicht
als ein genaueres Verfahren erscheinen, wenn man den Wert von 4B1B2
in Gleichung (7a) nach v integrierte, um die Summe der Schwebungen
in allen Corti'schen Organen zu erhalten. Dann müßte
man aber noch irgend eine wenigstens annähernde Kenntnis von der Dichtigkeit
der Corti'schen Organe für verschiedene Werte von v,
d. h. für verschiedene Teile der Skala haben, welche uns abgeht. In
der Empfindung kommt es jedenfalls mehr auf den stärksten Grad der
Rauhigkeit an, als auf die Ausbreitung schwächerer Rauhigkeit über
viele empfindende Organe. Ich habe deshalb vorgezogen, nur dag in (7b)
gegebene Maximum der Schwebungen zu berücksichtigen.
....................................................................(7b)
Ich habe mich bei Berechnung des Grades der Rauhigkeit, welche der Zusammenklang
zweier Töne gibt, die um das Intervall 2dvon
einander entfernt sind, damit begnügt den hier gefundenen Maximalwert
der Schwebungen zu berücksichtigen, welcher in dem am günstigsten
gelegenen Corti'schen Organe stattfindet. Allerdings werden schwächere
Schwebungen auch noch in den benachbarten Faserbögen erzeugt, aber
in schnell abnehmender Intensität. Es könnte deshalb vielleicht
als ein genaueres Verfahren erscheinen, wenn man den Wert von 4B1B2
in Gleichung (7a) nach v integrierte, um die Summe der Schwebungen
in allen Corti'schen Organen zu erhalten. Dann müßte
man aber noch irgend eine wenigstens annähernde Kenntnis von der Dichtigkeit
der Corti'schen Organe für verschiedene Werte von v,
d. h. für verschiedene Teile der Skala haben, welche uns abgeht. In
der Empfindung kommt es jedenfalls mehr auf den stärksten Grad der
Rauhigkeit an, als auf die Ausbreitung schwächerer Rauhigkeit über
viele empfindende Organe. Ich habe deshalb vorgezogen, nur dag in (7b)
gegebene Maximum der Schwebungen zu berücksichtigen.
Schließlich muß noch beachtet werden, daß sehr langsame
Schwebungen keine Rauhigkeit geben, daß diese bei gleicher Intensität
der Schwebungen und steigender Zahl ein Maximum erreicht, und dann wieder
abnimmt. um dies auszudrücken, muß der Wert von s
noch mit einem Faktor multipliziert werden, welcher gleich Null wird, wenn
die Zahl der Schwebungen sehr klein ist, welcher bei etwa 30 Schwebungen
sein Maximum erreicht, und dann wieder abnimmt, um für unendlich viel
Schwebungen wieder gleich Null zu werden. Wir setzen also die Rauhigkeit
r,
welche vom aten Oberton herrührt:
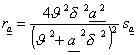 Der Faktor von s erreicht den Maximalwert l, wenn ad
= J wird, den Wert 0, wenn d
, welches den halben Abstand der beiden Töne in der Skala bezeichnet,
gleich 0 oder gleich ¥ wird. Da es gleichgültig
ist, ob dpositiv oder negativ ist, mußte
der Ausdruck zu einer geraden Funktion von
d
gemacht werden. Es ist der einfachste Ausdruck, der den gegebenen Bedingungen
genügt, er ist aber natürlich bis zu einem gewissen Grade willkürlich.
Der Faktor von s erreicht den Maximalwert l, wenn ad
= J wird, den Wert 0, wenn d
, welches den halben Abstand der beiden Töne in der Skala bezeichnet,
gleich 0 oder gleich ¥ wird. Da es gleichgültig
ist, ob dpositiv oder negativ ist, mußte
der Ausdruck zu einer geraden Funktion von
d
gemacht werden. Es ist der einfachste Ausdruck, der den gegebenen Bedingungen
genügt, er ist aber natürlich bis zu einem gewissen Grade willkürlich.
Für J ist die halbe Breite desjenigen
Intervalls zu setzen, welches in der Höhe des tieferen Grundtones
30 Schwebungen in der Sekunde gibt.
Da wir c' mit 264 Schwingungen als Grundton genommen haben,
ist gesetzt worden 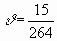 .
Es wird also schließlich:
.
Es wird also schließlich:
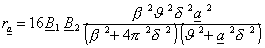 Nach dieser Formel sind nun für die Diagramme, Fig.
60 A und B, Seite 318,
die Rauhigkeiten der Intervalle berechnet worden, welche von den einzelnen
Obertönen herrühren, und einzeln über einander in die Zeichnung
eingetragen.
Nach dieser Formel sind nun für die Diagramme, Fig.
60 A und B, Seite 318,
die Rauhigkeiten der Intervalle berechnet worden, welche von den einzelnen
Obertönen herrühren, und einzeln über einander in die Zeichnung
eingetragen.
Wenn auch die Genauigkeit der Theorie noch manches zu wünschen
übrig läßt, so leistet dieselbe doch soviel, zu zeigen,
daß die von uns aufgestellte theoretische Ansicht eine solche Verteilung
der Dissonanzen und Konsonanzen, wie sie in der Natur vorkommt, wirklich
erklären kann.
Herr Alfred M. Mayer (Professor in Hoboken, New-Jersey)1)
hat Versuche über die Nachdauer der Gehörempfindung und die Anzahl
der hörbaren Schwebungen angestellt, indem er zwischen einer schwingenden
Stimmgabel und ihrem Resonator eine Scheibe mit Öffnungen, die der
des Resonators gleich gestaltet waren, umlaufen ließ, so daß
der Ton stark gehört wurde, wenn eine Öffnung der Scheibe vor
der des Resonators stand, schwach, wenn die letztere gedeckt war. Seine
Resultate stimmen im Wesentlichen mit den von mir auf Seite 234 bis 238
und 306 bis. 309 gemachten Annahmen, sind aber vollständiger durch
die ganze Skala verfolgt. Seine Angaben sind folgende:
|
|
Anzahl der Schwebungen
|
| Ton |
Schwingungszahl |
bei der die Unterbrechungen verschwinden |
für die stärkste Dissonanz |
| C |
64 |
16 |
6.4 |
| C |
128 |
26 |
10.4 |
| C' |
256 |
47 |
18.8 |
| G' |
384 |
60 |
24.0 |
| c" |
512 |
78 |
31.2 |
| e" |
640 |
90 |
36.0 |
| g" |
768 |
109 |
43.6 |
| c''' |
1024 |
135 |
54.0 |
1) Silliman's Journal, Ser. III, Vol. VIII, Octb.
1874. Philosophical Magazine. Mai 1875. Vol. IL.
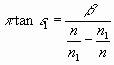 und
und 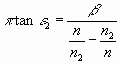
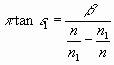 und
und 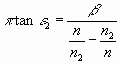
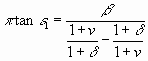 ,
, 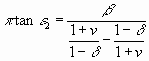
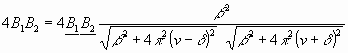 .................(7a)
.................(7a)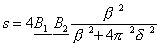 ....................................................................(7b)
....................................................................(7b)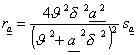
![]() .
Es wird also schließlich:
.
Es wird also schließlich: